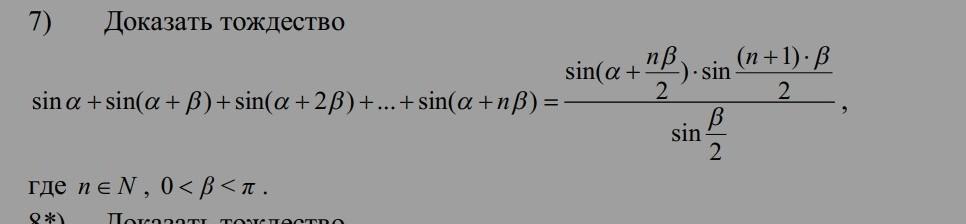Question

Докажите тождество.
см. вложение​

Answer 1

Ответ:

Объяснение:

7 ) Позначимо для зручності вираз лівої частини даної рівності

буквою А  та  домножимо і поділимо цей вираз на   sinβ/2 , далі перетворимо :

А =[sinαsinβ/2+sin(α+β)sinβ/2 +sin(α+2β)sinβ/2+...+sin(α+nβ)sinβ/2]:sinβ/2=

= 1/2[cos(α-β)-cos(α+β/2)+cos(α+β/2) - ...+cos(α+(2n-1)β/2) -

- cos(α+(2n+1)β/2)] /sinβ/2 = 1/2[ (cos(α - β) - cos(α+(2n+1)β/2)]/sinβ/2 =

= [ sin( n + 1 )/2 * sin ( α + nβ/2 ) ]/ sinβ/2 .

В результаті тотож. перетворень ми одержали праву частину даної

рівності . Отже , дана рівність є тотожністю .