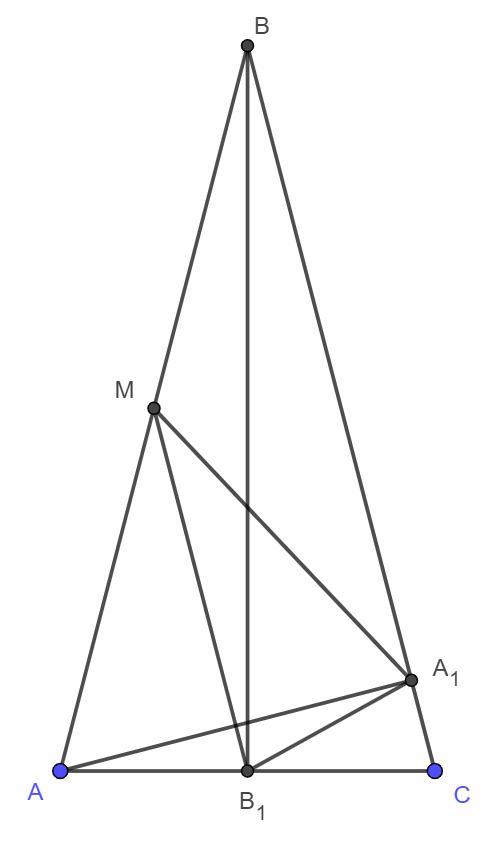
в треугольнике авс со сторонами ав=вс=4, и ас=2, проведены высоты аа1 и вв1. точка м- середина стороны ав. найдите периметр треугольника ма1в1
Alexandr130398:
P=(6+корень(34))/4
А где решение?
P = 5
ой, я подумал М-середина AB1. Хорошо, что не стал решение писать))
Ответы
Ответ дал:
9
Поскольку AB = BC, то ΔABC - равнобедренный ⇒ BB₁ - высота, биссектриса и медиана ⇒ AB₁ = B₁C = AC/2 = 1. Поскольку точка M - середина AB, то AM = BM = AB/2 = 2.
A₁M - медиана прямоугольного треугольника AA₁B ⇒ AM = BM = MA₁ = 2 (М - центр описанной окружности и равны как радиусы окружности). Аналогично, с прямоугольного треугольника AA₁C длина стороны B₁A₁ = AB₁ = B₁C = 1.
MB₁ - средняя линия треугольника ABC ⇒ MB₁ = 1/2BC = 2.
P(MA₁B₁) = MA₁ + A₁B₁ + MB₁ = 2 + 1 + 2 = 5.
Ответ: 5.
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад