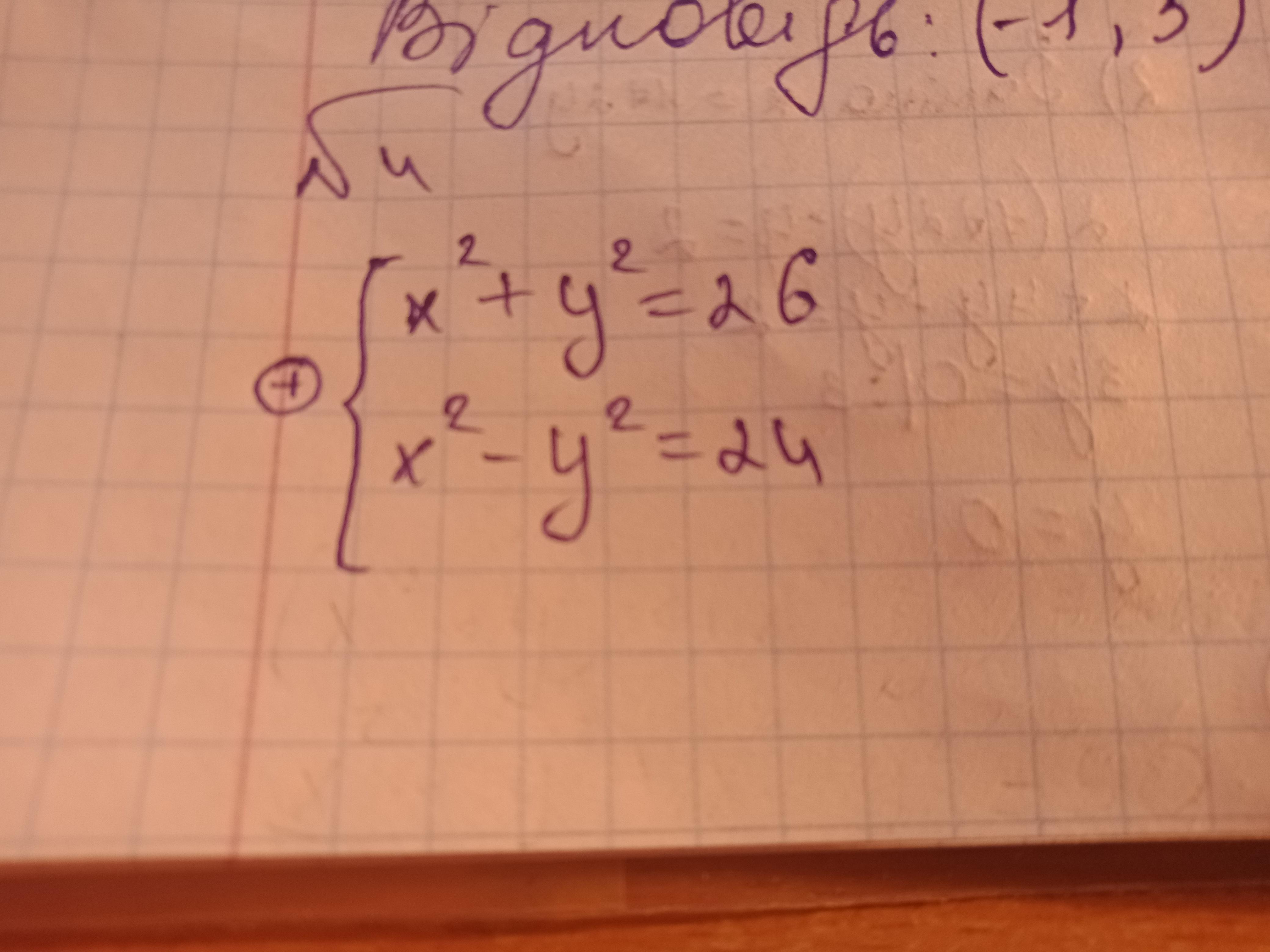Ответы
Ответ дал:
0
Ответ:
(-5; -1); (5; -1); (-5; 1); (5;1)
Объяснение:
Всего у данной системы уравнений будет 4 пары корней:
(-5; -1); (5; -1); (-5; 1); (5;1)
Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад