алгебра задание в закрепе! желательно сегодня! а лутше СЕЙЧАС!
Приложения:
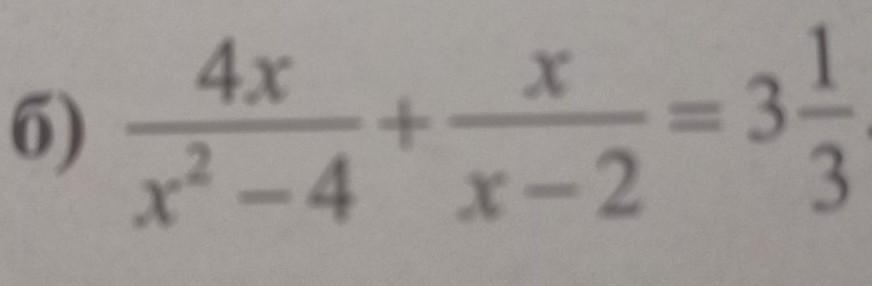
sooffiks:
правильно пишется *лучше
я знаю, просто спешил и опечатался
ну ладно, тогда
но все равно спасибо!
пожалуйста)
Ответы
Ответ дал:
1
Ответ:
или
Объяснение:
Полученное уравнение равносильно следующей системе
Решим квадратное уравнение:
Отсюда находим корни х1 и х2:
Оба значения х входят в ОДЗ - следовательно являются корнями исходного уравнения.
Запишем ответ:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад