ПОМОГИТЕ ПОЖАЛУЙСТА
Основы равносторонней трапеции равны 13 см и 77 см, а боковая сторона 40 см Вычислите в сантиметрах радиус описанной около трапеции круга?
dnepr1:
В задании: "равносторонней..." - должно, наверно, быть равнобокой?
Да
42,5
Ответы
Ответ дал:
1
BH - высота трапеции
AH =(AD-BC)/2 =(77-13)/2 =32
HD =77-32 =45
BH =√(AB^2 -AH^2) =24
BD =√(BH^2 +HD^2) =√(24^2 +45^2) =51
OT - серединный перпендикуляр к AB
∠ADB =∠AOB/2 =∠AOT (вписанный равен половине центрального)
△AOT~△BDH (по двум углам)
OA/BD =AT/BH => OA =51*20/24 =42,5 (см)
Или
Из треугольника ABH
cosA =AH/AB =4/5
sinA =√(1 -cosA^2) =3/5
Из треугольника ABD
BD^2 =AB^2 +AD^2 -2AB*AD*cosA (т косинусов) => BD=51
BD/sinA =2R => R=42,5 (т синусов)
Приложения:
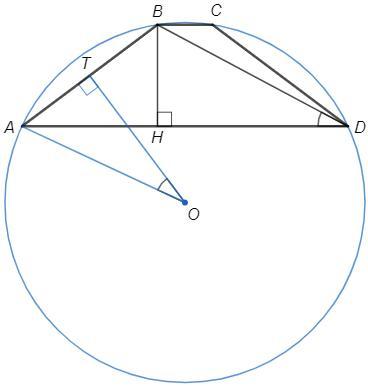
Есть ещё вариант: R = abc/4S, где S - площадь треугольника АВD.
Вас заинтересует
3 года назад
8 лет назад
8 лет назад