Question

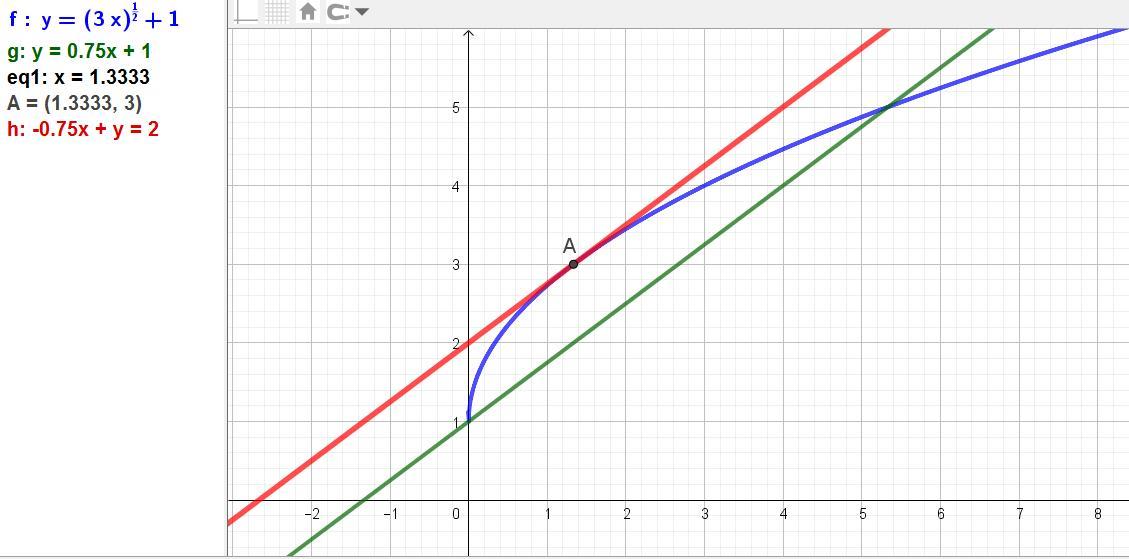
Составьте уравнение касательной к графику функции f(x)=√3x + 1, параллельной прямой y = 3/4x + 1.

Answer 1

Производная функции равна угловому коэффициенту касательной.

Находим производную: y' = (√(3x) + 1)' = √3/2√x.

Приравняем производную значению 3/4.

√3/2√x = 3/4.

6√x = 4√3.

√x = (4/6)√3, возведём в квадрат.

х = 48/36 = 4/3. Это абсцисса точки касания.

Найдём её ординату.

у = √(3*(4/3) + 1 = 2 + 1 = 3.

Уравнение касательной:

у = (3/4)(х - (4/3)) + 3 = (3/4)х - 1 + 3 = (3/4)х + 2.

Ответ: (3/4)х + 2.