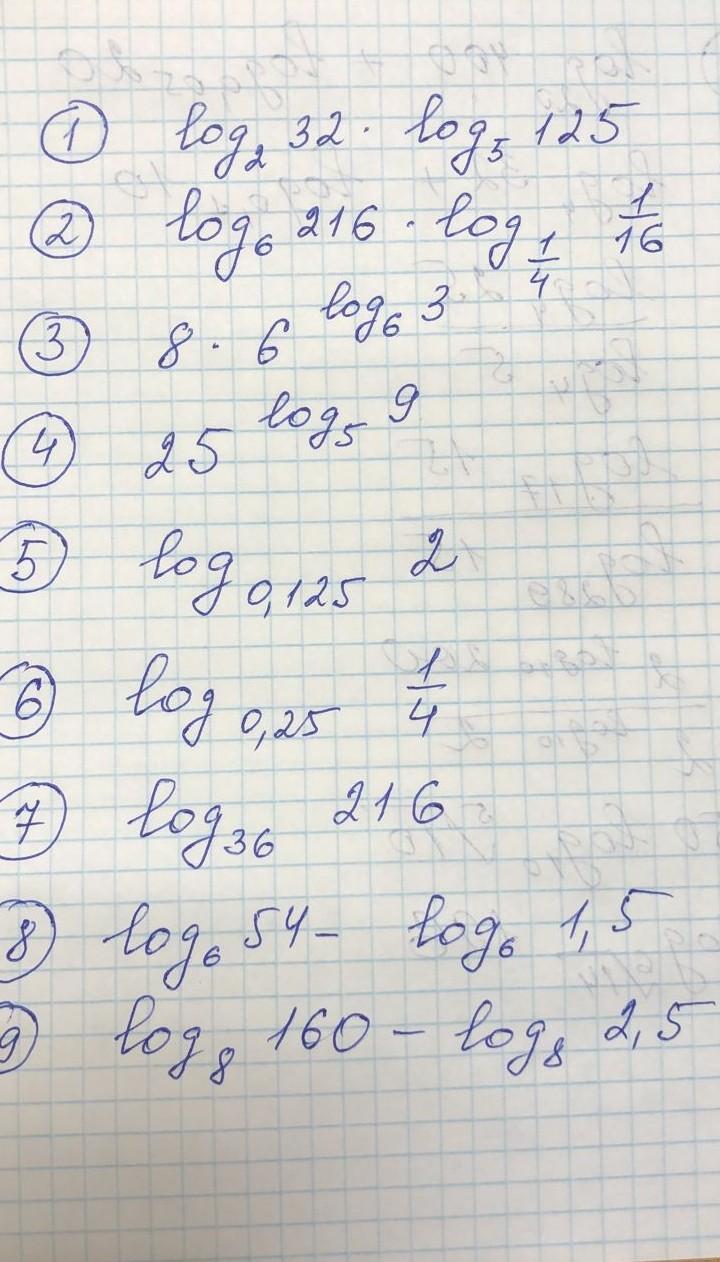Question

Помогите решить логорифмы. ​

Answer 1

Ответ:

Пошаговое объяснение:

1)log2^32*log5^125=5*3=15 Пример как писать:㏒$2^{32}$ · ㏒$5^{125\\}$

2)log6^216*log1/4^1/16=3*2=6        

3)8* 6^log6^3=8*3=24       Пример как писать:  $6^{log\frac{1}{4} ^{\frac{1}{16} }$

4)25^log5^9=5^2log5^9= 5^log5^9^2= 9^2=81

5)log 0.125^2=log1/8^2=log2^-3^2=1/-3 * log2^2= -1/3

6)log 1/4^1/4=1

7)log36^216=log6^2^6^3=3/2log6^6= 3/2

8)log6^54 - log6^3/2=log6^54/ 3/2= log6^108/3=log6^36=2

9)log8^160 - log8^5/2=log8^64=2