Решить данные задания. Даю 100 баллов.
Приложения:
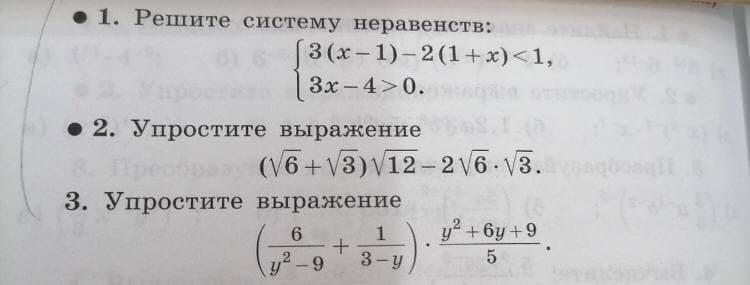
4ekHyTbI:
2.6
2.6
3. -27y2+81-6y3+u2y2+6u2y+9u2
3. -27y2+81-6y3+u2y2+6u2y+9u2
нет пошагового решения.
Ответы
Ответ дал:
3
Ответ:
Объяснение:
1.
Ответ:
2.
3.
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад