Question

пожалуйста 100 баллов!!!!!!!!!!!!!

Из точки к плоскости проведены две наклонные.

На рисунке 124 прямая АД перпендикулярна плоскости А.

Найдите длину отрезка АД, если наклонные равны 17 и 25 см, а разность их ортогональных проекций равна 12 см.

Answer 1

Ответ:

AD = 15 см.

Объяснение:

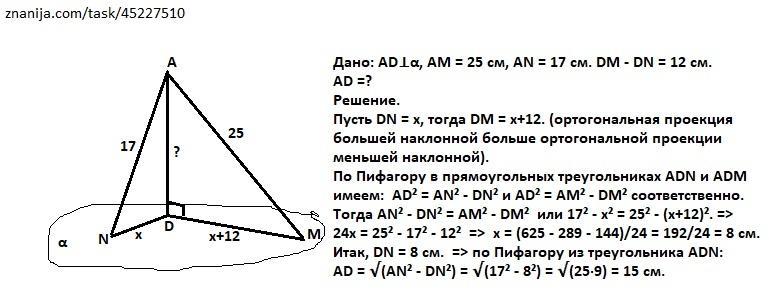
Дано: AD⊥α, AN = 17 см. AM = 25 см.  DM - DN = 12 см.

Найти AD.

Решение.

Пусть DN = x, тогда DM = х+12. (ортогональная проекция большей наклонной больше ортогональной проекции меньшей наклонной).

По Пифагору в прямоугольных треугольниках ADN и ADM имеем:  AD² = AN² - DN² и AD² = AM² - DM² соответственно.

Тогда AN² - DN² = AM² - DM²  или 17² - х² = 25² - (х+12)². =>

24х = 25² - 17² - 12²  =>  х = (625 - 289 - 144)/24 = 192/24 = 8 см.

Итак, DN = 8 см.  => по Пифагору из треугольника ADN:

AD = √(AN² - DN²) = √(17² - 8²) = √(25·9) = 15 см.