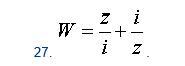Ответы
Ответ дал:
1
Ответ:
Пошаговое объяснение:
Подставим в функцию:
Очевидно, дифференцируемы
.
Запишем условия Коши-Римана:
Т.е. условия Коши-Римана выполнены для .
Значит, функция дифференцируема в
.
princesscelestia85:
здравствуйте, можете мне пожалуйста помочь с информатикой?
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад