Question

100 баллов! Срочно! С подробным пошаговым решением. Решить систему уравнений
${x}^{3} - {y}^{3} = - 7 \\ 3x {y}^{2} - 3 {x}^{2} y = 5 \sqrt{2}$
​

Answer 1

Ответ:

Объяснение:

$\left \{ {{x^3-y^3=-7} \atop {3xy^2-3x^2y=5\sqrt{2} }} \right.$

сложим эти два уравнения и преобразуем по формуле куба разности:

$x^3-y^3+3xy^2-3x^2y =5\sqrt{2}-7 \right.\\x^3-3x^2y +3xy^2-y^3=5\sqrt{2}-7 \right.\\(x-y)^3=5\sqrt{2}-7$

Для простоты вычислений введём константу С

$C=\sqrt[3]{5\sqrt{2}-7 }$

C≈0,4142

Из последнего выражения имеем следующие тождества

$x-y=C\\x = y+C$

Подставляем x в первое уравнение

$(y+C)^3-y^3=-7\\y^3+3y^2C+3yC^2+C^3-y^3=-7\\3y^2C+3yC^2+C^3+7=0$

В последнее С³ подставим его значение, чтобы сократить семёрку.

$3y^2C+3yC^2+5\sqrt{2}-7 +7=0\\3y^2C+3yC^2+5\sqrt{2}=0$

Теперь решаем обычное квадратное уравнение

$y_{12} =\frac{-3C^2\pm\sqrt{(3C^2)^2-4*2C*5\sqrt{2} } }{2*3*C} \\y_{12} =\frac{-3C^2\pm\sqrt{9C^4-40C\sqrt{2} } }{6C}$

Тут получается что дискриминант отрицательный и корней нет.

Вариант второй, графический

из первого уравнения получаем график функции

$y=\sqrt[3]{x^{3} +7}$

А из второго

$3xy^2-3x^2y=5\sqrt{2} \\3xy^2-3x^2y-5\sqrt{2} =0\\y_{12} =\frac{3x^3\pm\sqrt{9x^4+60x\sqrt{2} } }{6x}$

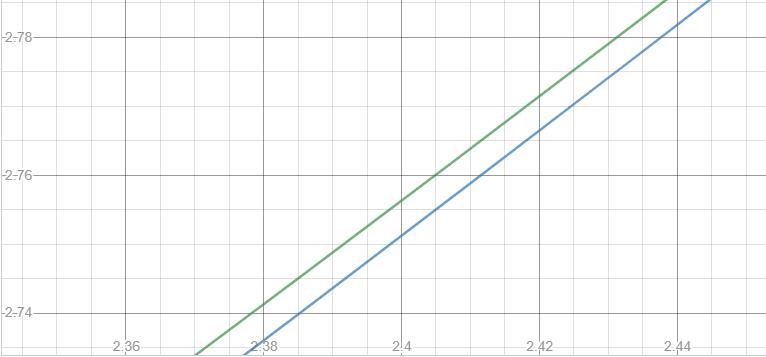
Строим графики.

Видим, что точек пересечения нет.

Графики стремятся приблизится друг к другу, но не пересекаются