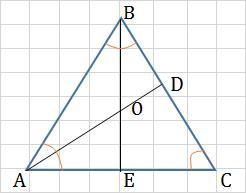
В равносторонние треугольнике ABC биссектрисы AD и BE пересекаются в точке O. Найдите угол AOE между биссектриса и треугольника ABC
Ответы
Ответ дал:
11
Ответ:
Объяснение:
1) В равностороннем треугольнике все углы равны между собой и = 60°
2) Биссектриса в равностороннем треугольнике является также его медианой и высотой, поэтому ВЕ ⊥ АС и, следовательно, ∠ВЕА = 90°
3) Рассмотрим ΔАОЕ.
∠ВЕА = 90°
∠ОАЕ = 60°/2 = 30° (т.к. АD - биссектриса ∠А и , значит, делит этот угол пополам)
Теорема: Сумма всех углов треугольника равна 180º,т.е.
∠ВЕА + ∠ ОАЕ + ∠АОЕ = 180°
90° + 30° + ∠АОЕ = 180°, откда
∠АОЕ = 180° - 120° = 60°
Приложения:
sken72713:
спасиба мамог
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад