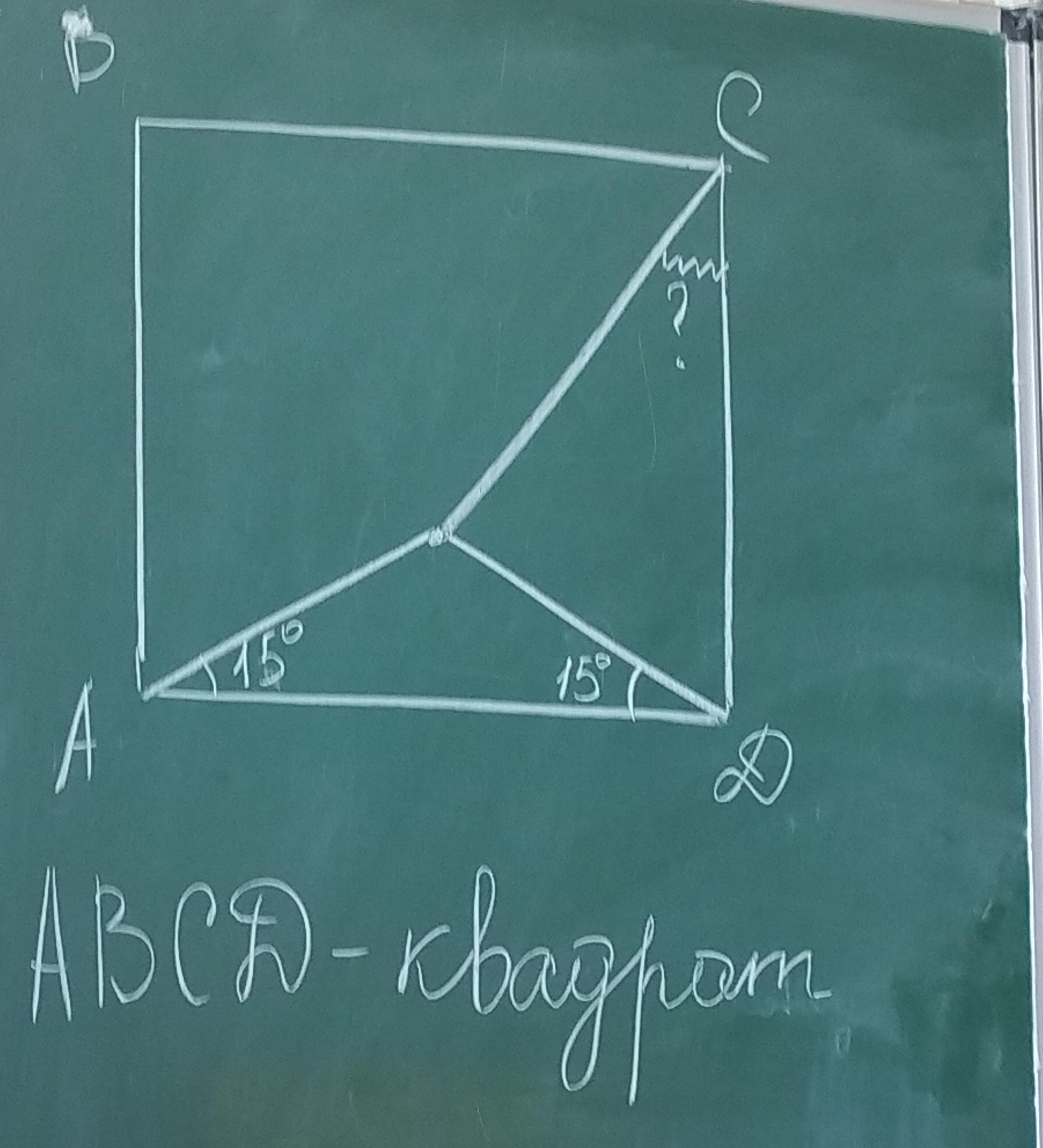Question

Срочно!!!! Даю 35 балів

Answer 1

Пусть точка пересечения отрезков внутри квадрата - это точка К.

Примем длину стороны квадрата за 1.

Опустим перпендикуляры из точки К на стороны квадрата АД и СД - пусть это точки Е и Н.

Точка Е делит сторону АД пополам (треугольник АКД - равнобедренный). ДЕ = 1/2.

КЕ = ДЕ*tg 15°.

Тангенс 15 градусов как половина от 30 равен 2 - √3.

Поэтому отрезки КЕ = ДН = (2 - √3)/2 = 1 - (√3/2).

Отрезок СН стороны СД равен 1 - ДН = 1 - (1 - (√3/2)) = √3/2.

Определяем тангенс искомого угла (пусть α).

tgα = КН/СН = (1/2)/(√3/2) = 1/√3.

Тогда угол α = arctg(1/√3) = 30 градусов.

Ответ: искомый угол равен 30 градусов.