Question

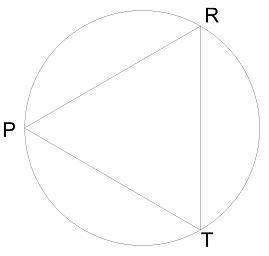
Треугольник PRT — равнобедренный, RT — основание треугольника, дуга окружности RT= 60°.

(фото)

Вычисли углы треугольника:

∢ P=
°;

∢ R=
°;

∢ T=
°.

Answer 1

Ответ: Углы в ΔPRT 30°; 75°; 75°.

Объяснение:

Градусная мера дуги равна градусной мере соответствующего центрального угла. Тч.О - центр окружности. Центральный угол ∠ROT = 60°.

Вписанный угол равен половине соответствующего центрального угла. ∠P = 30°.

ΔRPT равнобедренный с основанием RT. В равнобедренном треугольнике углы при основании равны. ∠T = ∠R = (180° - 30°)/2 = 75°.

Углы в ΔPRT 30°; 75°; 75°.