Ответы
Ответ:
Объяснение:
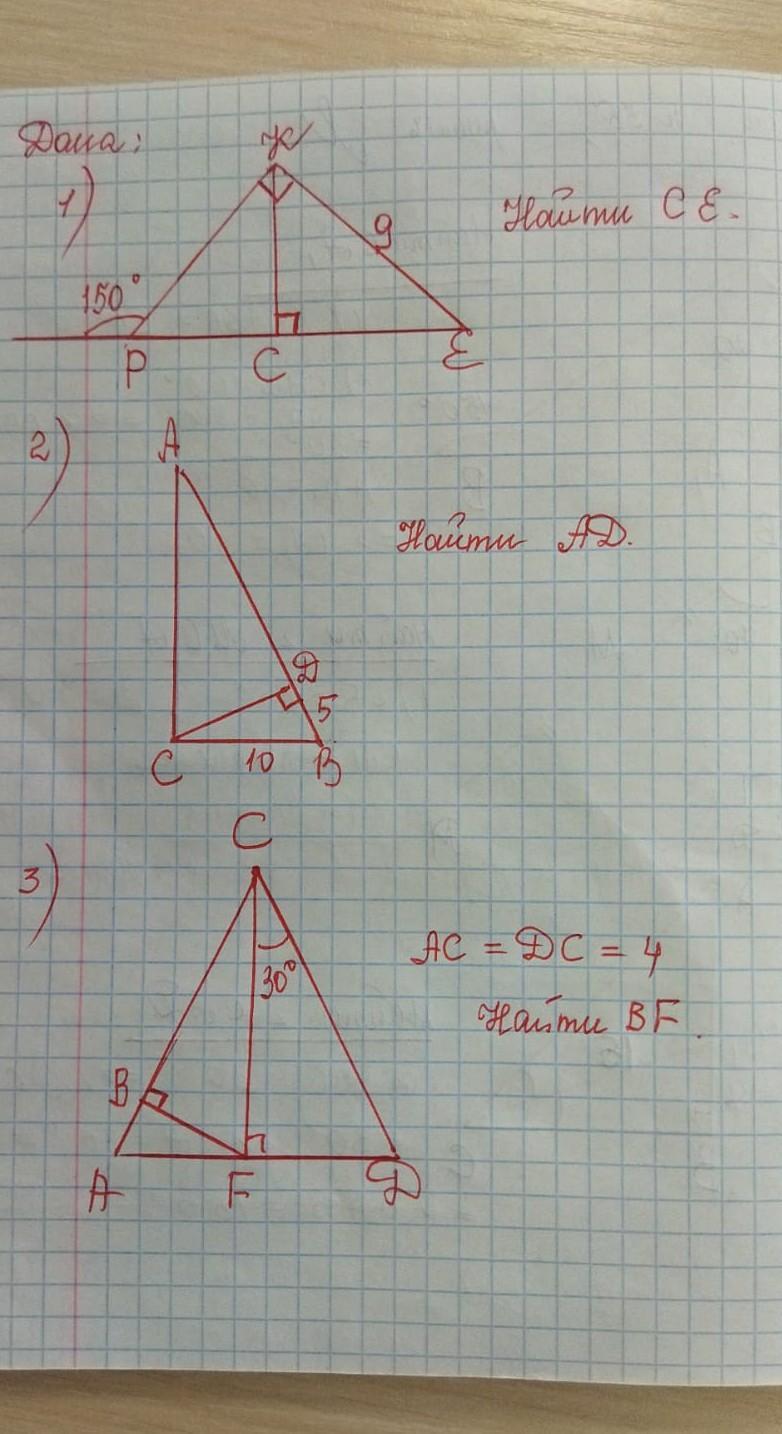
1) ∠150° и ∠КРС - смежные, их сумма = 180°, следовательно,
∠КРС = 180° - 150° = 30°
ΔРКЕ - прямоугольный по условию, поэтому
∠КЕР = 180° - 30° - 90° = 60°
ΔКСЕ - прямоугольный по условию,
∠СКЕ = 180° - 90° -∠КЕС = 90° - 60° = 30°
В прямоугольном треугольнике против угла в 30° лежит катет, равный половине гипотенузы:
СЕ = 9 /2 = 4,5(см)
2) ΔСЕВ - прямоугольный по условию, DВ = ¹/₂СВ = 5 /10 = 1/2, значит,
∠DCB = 30°, а ∠DBC = 60°
Рассмотрим ΔСАВ.
∠С = 90°, ∠ABC = 60°, следовательно, ∠А = 90° -60° = 30°
Против угла в 30° лежит катет, равный половине гипотенузы:
АВ = 2СD = 2 *10 = 20(см)
АD = 20 - 5 = 15(см)
3) АС = DC по условию, т.е. ΔACD - равнобедренный, В равнобедренном Δ-ке высота, проведенная к основанию, является биссектрисой и медианой.
СF - высота по условию, а также биссектриса и медиана.
∠ACF = ∠FCD = 30°
В ΔАСВ ∠А = 90° и FD = CD/2 = 4/2 = 2 (т.к. FD лежит против ∠ в 30°)
CF² = CD² - FD° (теорема: квадрат гипотенузы равен сумме квадратов катетов)
СF² = 4² - 2² = 12
CF = √12 = √4*3 = 2√3
Обратимся к ΔСBF. Он прямоугольный и ∠BCF = 30°, значит,
BF = CF/2 = 2√3/2 = √3