найдите площадь круга,вписанного в равнобедренный треугольник с боковой стороной а и углом а,противолежащим к основанию
Ответы
Ответ дал:
0
без фотика туговато. все корни и дроби ужасны ^1/2 это корень
Приложения:

Ответ дал:
0
Ответ:
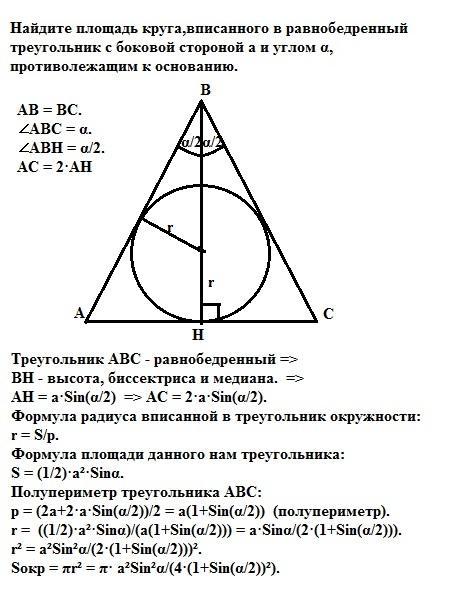
Sокр = πr² = π· а²Sin²α/(4·(1+Sin(α/2))²).
Объяснение:
Треугольник АВС - равнобедренный =>
ВН - высота, биссектриса и медиана. =>
AH = a·Sin(α/2) => AC = 2·a·Sin(α/2).
Формула радиуса вписанной в треугольник окружности:
r = S/p.
Формула площади данного нам треугольника:
S = (1/2)·a²·Sinα.
Полупериметр треугольника АВС:
p = (2a+2·a·Sin(α/2))/2 = а(1+Sin(α/2)).
r = ((1/2)·a²·Sinα)/(а(1+Sin(α/2))) = a·Sinα/(2·(1+Sin(α/2))).
r² = а²Sin²α/(2·(1+Sin(α/2)))².
Sокр = πr² = π· а²Sin²α/(4·(1+Sin(α/2))²).
Приложения:
Вас заинтересует
2 года назад
2 года назад
11 лет назад
11 лет назад