Question

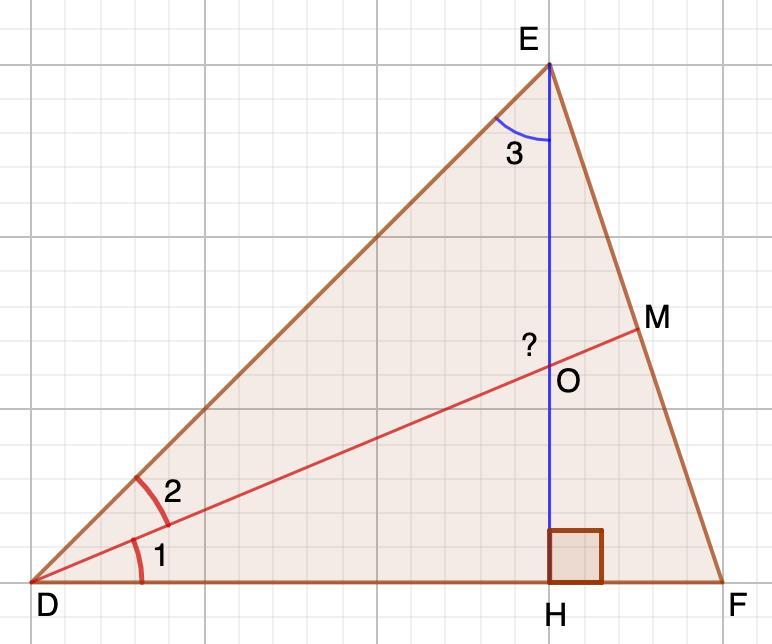
В остроугольном треугольнике DEF EH – высота, DM – биссектриса, O – точка пересечения прямых EH и DM, угол EDF равен 280. Найдите угол DOE. Ответ дайте в градусах

Answer 1

Ответ:

104°

Объяснение:

Дано: Δ DEF

EH - высота; DM - биссектриса

∠EDF=28°

Найти: ∠DOE

Решение:

1. Рассмотрим ΔDEH - прямоугольный (EH - высота)

• Сумма углов  треугольника равна 180°

∠3=180°-(∠EDF+∠EHD)=180°-(28°+90°)=62°

2. Рассмотрим ΔDOE.

∠2=∠1=∠EDF:2=28°:2=14° (DM - биссектриса)

∠DOE=180°-(∠2+∠3)=180°-(14°+62°)=104°