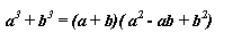1.Докажите, что 35^3 + 75^3 делится на 110
2.Найдите все натуральные m, при которых выражение 3m+8/m является натуральным числом
3.Найдите последнюю цифру числа 8^2011, 2^2167
Ответы
Объяснение:
1. 35^3 + 75^3
Есть формула сокращенного умнажения(ФСУ) сумма кубов. см. в картинке. Тогда получаем.
35^3+75^3=(35+75)(35^2-35*75+75^2)=110(35^2-35*75+75^2)
Тогда при делении на 110 множитель 110 исчезает.
2. 3m+8/m
Натуральные числа это число используемые при счёте, причем ноль не входит. Например: 1, 2, 3, 4, 5, 6...
3*1+8/1=11
3*2+8/2=7
3*4+8/4=14
3*8+8/8=25
Ответ: 1, 2, 4, 8.
3. 8^2011
при возведении в степень. Последняя цифра повторяется с периодичностью 4.
8^1=8
8^2=64
8^3=512
8^4=4096
8^5=32768
8^6=262144
8^7=2097152
8^8=16777216
8^9=134217728
...
Делим 2011 на 4, получаем остаток 3. Тогда последняя цифра 2.
Ответ: 2.
2^2167
При возведении в степень. Последняя цифра повторяется с периодичностью 4.
2^1=2
2^2=4
2^3=8
2^4=16
2^5=32
2^6=64
2^7=128
...
Делим 2167 на 4, получаем остаток 3. Последняя цифра 8.
Ответ: 8.