Ответы
Ответ дал:
1
Ответ:
Объяснение:
4-5-6 решено
Приложения:
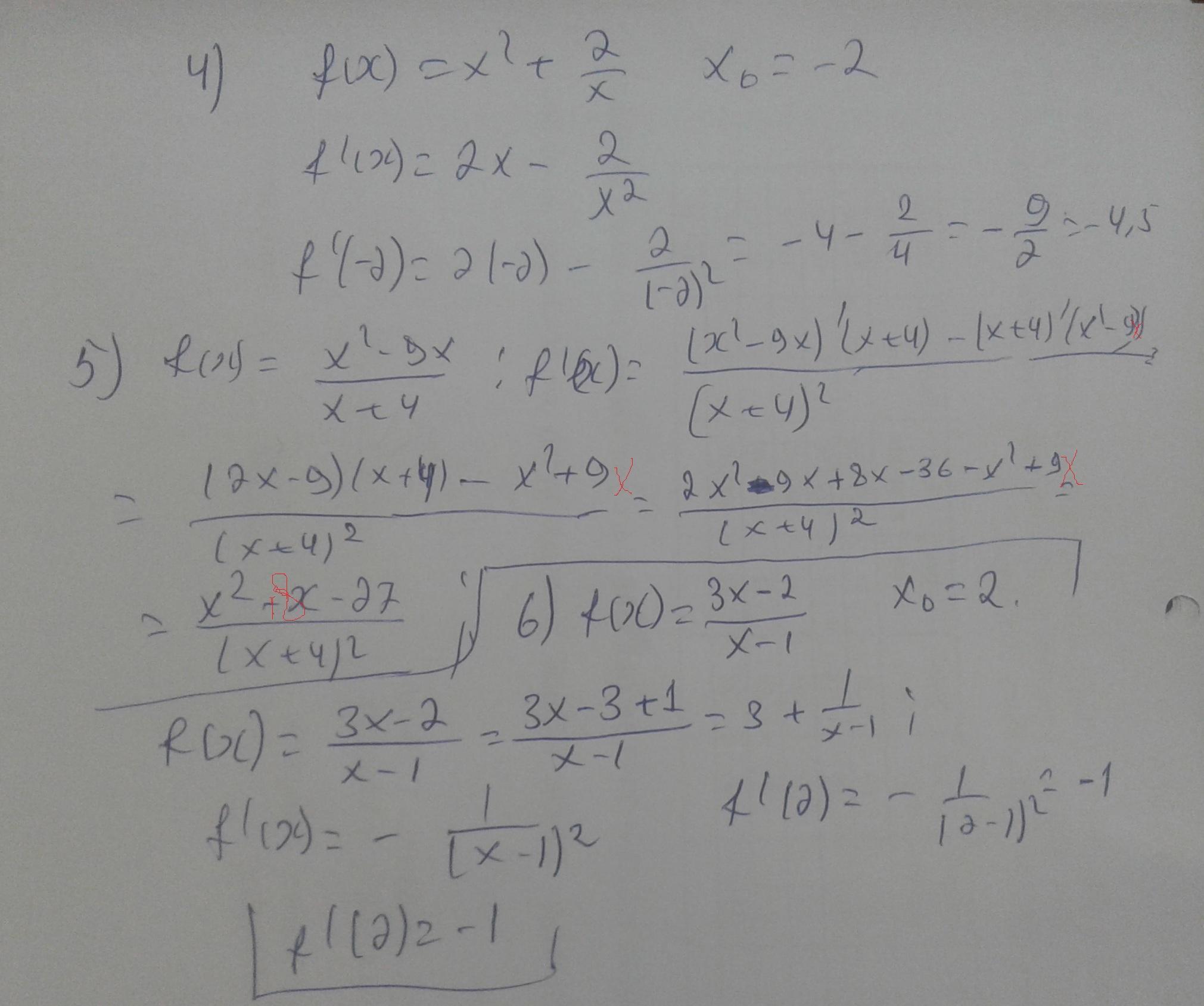
В пятом примере в самом начале потеряли x: должно быть x² – 9x, у вас x² – 9.
Ответ дал:
1
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад