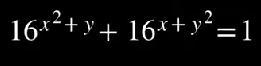Ответы
Ответ дал:
2
причем неравенство превращается в равенство тогда и только тогда, когда
Ответ:
mvolturi:
здравствуйте, можете помочь пожалуйста с одним уравнением? https://znanija.com/task/45409725
Ответ дал:
2
Ответ:
Объяснение:
сумма двух неотрицательных слагаемых ≤ 0
возможно только равенство 0 если каждое слагаемое равно 0
здравствуйте, можете помочь пожалуйста с одним уравнением? https://znanija.com/task/45441904
Вас заинтересует
2 года назад
3 года назад
8 лет назад
10 лет назад
10 лет назад