Question

Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4 : 1, считая от вершины острого угла. Найди большую сторону параллелограмма, если его периметр равен 36.

Answer 1

Ответ: 10

Объяснение:

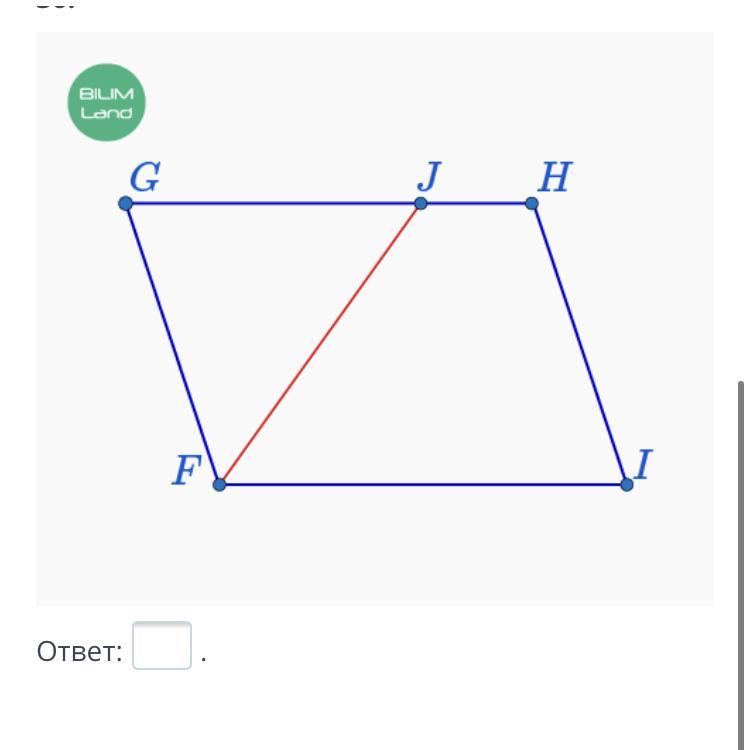
Пусть GJ = 4x, тогда JH = 1x.

Биссектриса параллелограмма отсекает от него равнобедренный треугольник.  Значит треугольник FGJ - равнобедренный.

Тогда: GJ = GF = 4x.

Периметр параллелограмма можно вычислить по формуле : P(GFIH) = 2(GH+GF).

36= 2(4x+4x+1x)

36= 9x*2

36= 18x

x= 36/18

x=2

Большая сторона GH = 4x+1x = 5x = 10