Сторона основания правильной четырехугольной пирамиды равна 10 см, а угол между боковым ребром и плоскостью основания составляет 60 °. Найдите высоту пирамиды. Пожалуйста подробно с рисунком.
Ответы
Ответ дал:
3
Объяснение:
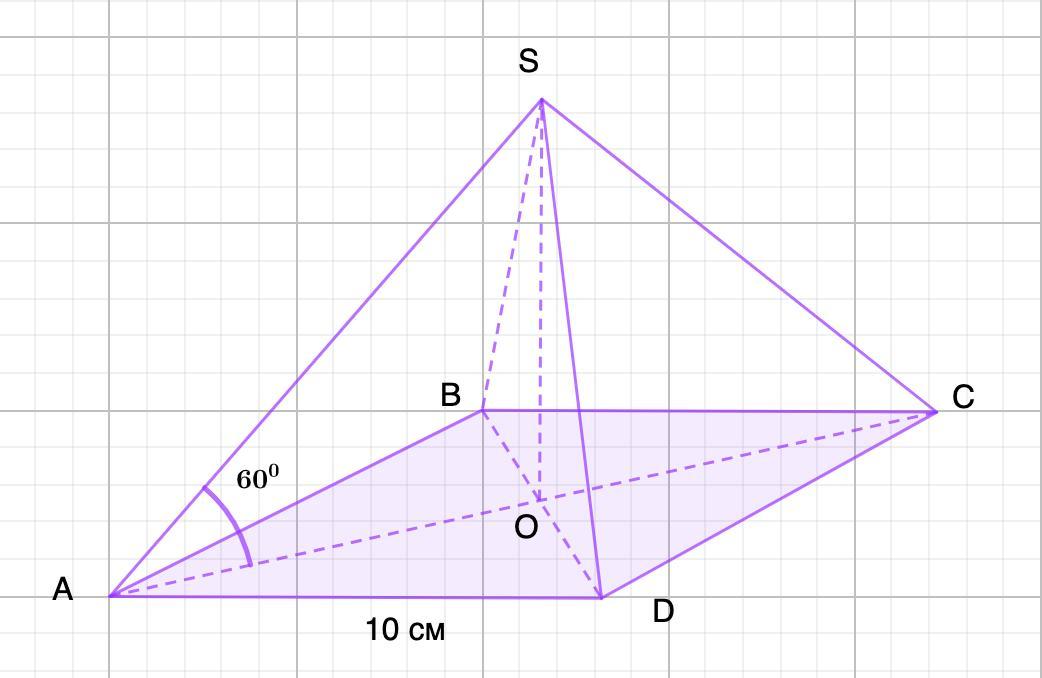
Дано: SABCD - правильная четырехугольная пирамида.
∠SAC = 60°
AD=10 см
Найти: SO
Решение:
1. Рассмотрим ΔACD - прямоугольный. ( в основании - квадрат)
По теореме Пифагора:
(см)
АО = ОС = 10√2:2 = 5√2 (см)
2. Рассмотрим ΔASO - прямоугольный.
- Сумма острых углов прямоугольного треугольника равна 90°.
∠ASO = 90° - ∠SAO = 90° - 60° = 30°
- Катет, лежащий против угла 30° равен половине гипотенузе.
⇒ AS = 2 AO = 5√2·2=10√2 (см)
По теореме Пифагора
(см)
Приложения:
lola67851:
Спасибо вам
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад