Алгебра. Даю 15 баллов. Нужно решить все уравнения через дискриминант и теорему Виета. Решать и тем и тем способами. Особенно подробно расписать 5 пример
Приложения:
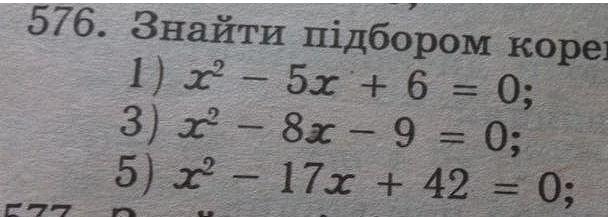
Ответы
Ответ дал:
1
Ответ:
Объяснение:
Через дискриминант:
Через теорему Виета:
Через дискриминант:
Через теорему Виета:
Через дискриминант:
Через теорему Виета:
Miа16:
Большое спасибо))
Пожалуйста )
Вас заинтересует
2 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад