помогите, пожалуйста, срочно!
Вычислить несобственный интеграл или установить его расходимость.
Приложения:
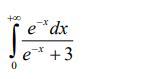
Ответы
Ответ дал:
1
Ответ:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад