Question

Катеты прямоугольного треугольника равны 21 см и 28 см.
Определи длину медианы, проведённую к гипотенузе этого треугольника.

Answer 1

Дано:

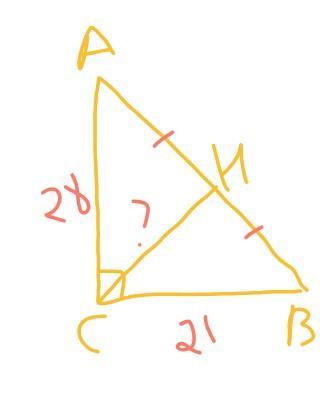
тр-к АВС, уг. С = 90°

АС = 28, ВС = 21

СН — медиана, АН = НВ

Найти: СН

Решение:

1. По свойству прямоугольного тр-ка, медиана, проведённая к гипотенузе, равна её половине.

АВ² = АС² + ВС² (т. Пифагора),

Тогда:

СН = АВ/2 = √(АС² + ВС²)/2

$ch = \frac{ \sqrt{( {28}^{2} + {21}^{2}) } }{2} = \frac{ \sqrt{(784 + 441} )}{2} = \frac{ \sqrt{1225} }{2} = \frac{35}{2} = 17.5$

Ответ: 17,5