ОПЯТЬ ГЕОМЕТРИЯ КООРДИНАТЫ 90 БАЛЛОВ ИНТЕРНЕТУРОК
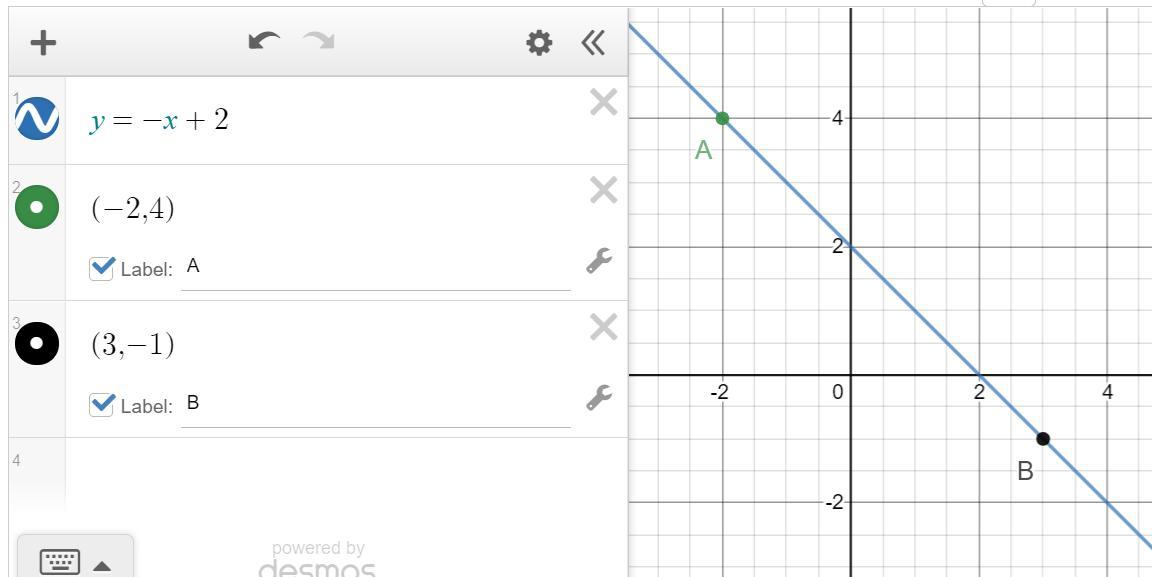
Запишите уравнение прямой, проходящей через точки A (-2; 4), B (3, -1). Найдите точки пересечения данной прямой с осями абсцисс и ординат.
Ответы
Ответ дал:
47
Ответ:
Объяснение:
Уравнение прямой
y = kx+b
Подставив две точки в уравнение получем систему
Вычитаем их первого уравнения второе
4 - (-1) =-2k + b - ( 3k + b )
4 + 1 = -2k + b - 3k - b
5 = -5k
k = -1
Подставляем еще k в первое уравнение с координатой кочки
4 = -2*(-1)+b
4 = 2 + b
b = 2
Итого имеем уравнение прямой
y = -x+2
Точки пересечения с осями будут
y = 2
x = 2
Приложения:
stepafrolof796:
Помоги пж с геометрией
Самый лучший человек вообще спасибо тебе огромное
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
10 лет назад