Ответы
Ответ дал:
1
Ответ:
Периметр параллелограмма равен 17,2 см
Объяснение:
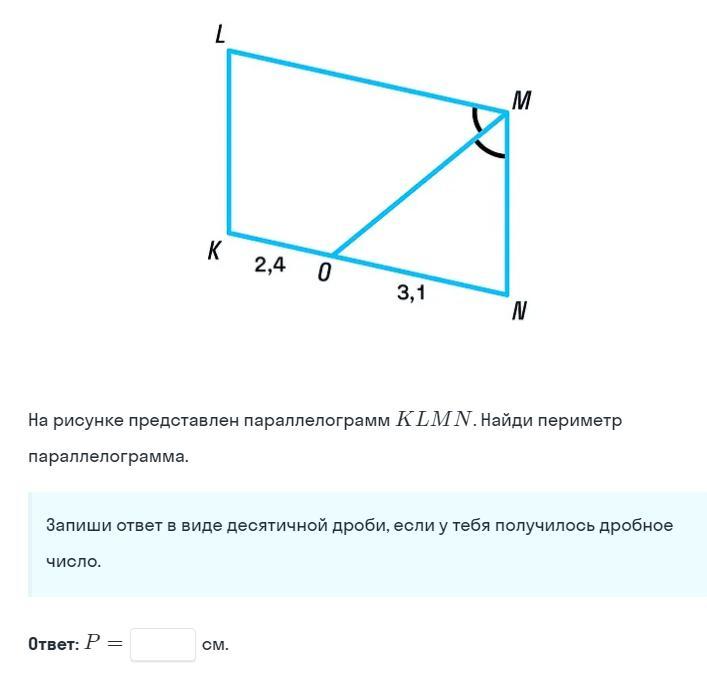
KLMN - параллелограмм. KO=2,4 см, ON = 3,1 см. ∠LMO=∠NMO.
- Параллелограмм это четырёхугольник, у которого противоположные стороны попарно параллельны и равны.
Так как ∠LMO=∠NMO, то МО - биссектриса ∠LMN параллелограмма KLMN.
Свойство биссектриса параллелограмма:
- Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
Действительно, ∠LMO=∠NOM - как внутренние накрест лежащие углы при параллельных прямых LM и KN и секущей MO. Следовательно ∠NOM = ∠NMO, а △MNO - равнобедренный.
В равнобедренном треугольнике боковые стороны равны: MN=ON=3,1 см
KN = KO + ON = 2,4 +3,1 = 5,5 см
- Периметр параллелограмма равен удвоенной сумме двух его смежных сторон.
P = 2•(KN+MN) = 2•(5,5+3,1)=2•8,6 = 17,2 см
#SPJ3
Вас заинтересует
2 года назад
3 года назад
8 лет назад
10 лет назад