Question

ЗАДАНИЕ 7!
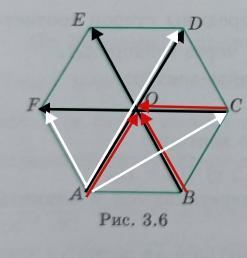
диагонали правильного шестиугольника ABCDEF пересекаются в точке О. Укажите вектор, равный вектору 1/2AD - 1/2CF + 1/2BE, началом и концом которого являются вершины этого шестиугольника. (рис. 3.6.)​

Answer 1

Ответ:

$\overrightarrow{AD}$

Пошаговое объяснение:

прежде всего определимся с нашими половинами векторов.

определение:

Произведением вектора $\vec{a}$ на число k называется вектор, получающийся из вектора $\vec {a}$ растяжением (при k > 1) или сжатием (при k <1 ) в k раз, причём направление вектора $\vec {a}$ сохраняется, если k >0  , и меняется на противоположное, если k <0 .

Итак наши вектора

$\displaystyle \frac{1}{2} \overrightarrow {AD} = \overrightarrow {AO}\qquad \quad\frac{1}{2} \overrightarrow {CF}= \overrightarrow {CO}\qquad \quad \frac{1}{2} \overrightarrow {BE}= \overrightarrow {BO}$

Теперь будем вычитать

$\displaystyle \overrightarrow {AO}- \overrightarrow {CO}= \overrightarrow {AO}+(-\overrightarrow {CO})= \overrightarrow {AO}+\overrightarrow {OC}=\overrightarrow {AC}$ ,

а теперь складывать.

Перенесем $\overrightarrow {BO}$  параллельно до точки начала $\overrightarrow {AC}$ и по правилу параллелограмма получим результат

$\overrightarrow {AC}+\overrightarrow {BO}=\overrightarrow{AD}$

ответ

$\overrightarrow{AD}$