Question

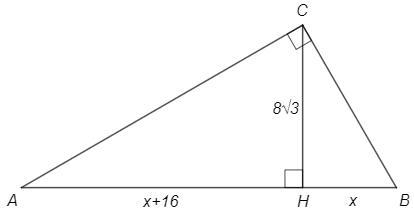
В прямоугольном треугольнике высота, проведенная к гипотенузе, равна 8√3 и делит гипотенузу на отрезки, разность длин которых равна 16. Найдите площадь треугольника.​

Answer 1

Высота из прямого угла (C) делит треугольник на два подобных друг другу и исходному.

△ACH~△ABC~△CBH

AH/CH=CH/BH => CH^2 =AH*BH => CH =√(AH*BH)

Доказали: Высота из прямого угла равна среднему пропорциональному проекций катетов на гипотенузу.

BH=x, AH=x+16, CH=8√3

CH^2 =AH*BH => 64*3 =x(x+16) => x^2 +16x -192 =0 => x=8 (x>0)

AB =8+8+16 =32

S(ABC) =1/2 AB*CH =1/2 *32 *8√3 =128√3