Question

Відстань від точки перетину діагоналей прямокутника до його суміжних сторін
дорівнює 4,9 см та 3,3 см.
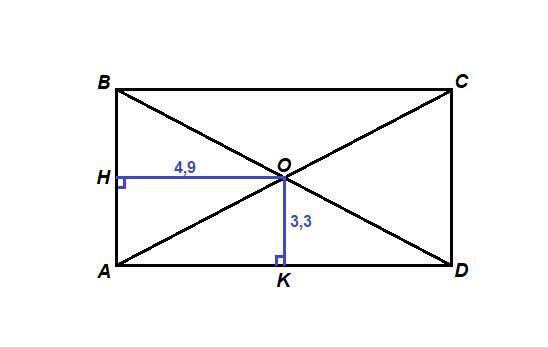
Накресли малюнок і обчисли периметр прямокутника.

Answer 1

Ответ:

32,8 см

Объяснение:

Расстояние от точки до прямой - длина перпендикуляра, проведенного из точки к прямой.

О - точка пересечения диагоналей.

Проведем ОН⊥АВ,

ОН = 4,9 см - расстояние от точки О до АВ.

Проведем ОК⊥AD,

ОК = 3,3 см -  расстояние от точки О до АD.

Диагонали прямоугольника равны и точкой пересечения делятся пополам, значит ОА = ОВ = ОС = OD.

ΔАОВ - равнобедренный, высота ОН является медианой,  ⇒

Н - середина АВ.

Тогда ОН - средняя линия треугольника АВС,

ВС = 2ОН = 2 · 4,9 = 9,8 см

ΔAOD - равнобедренный, высота ОК является медианой,  ⇒

К - середина AD.

Тогда ОК - средняя линия треугольника ABD.

АВ = 2ОК = 2 · 3,3 = 6,6 см

Периметр прямоугольника:

P = 2(AB + BC) = 2(9,8 + 6,6) = 2 · 16,4 = 32,8 см