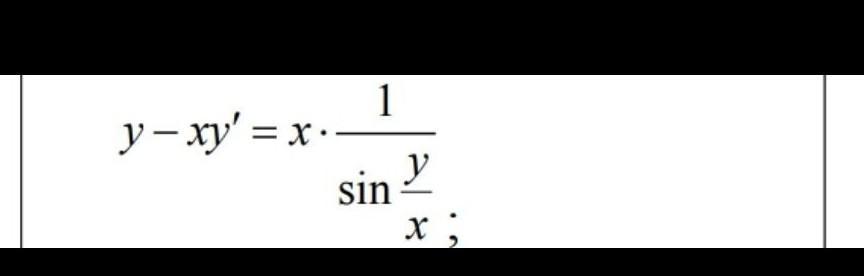Ответы
Ответ дал:
0
Ответ:
Объяснение:
я просто запишу всё решение подряд. надеюсь, разберетесь
умножим обе части на sin(v(x))
теперь можем интегрировать
теперь вернемся к замене y(x) = xv(x)
Аноним:
спасибо большое
инграли тоже помогите
там очень много писать. ждите. напишу
хорошо, а второе сама решила можете только первое с лева
ну, я уже всё решила. забирайте -)))
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
9 лет назад