Question

СРОЧНО, ДАЮ 70 БАЛЛОВ!!!
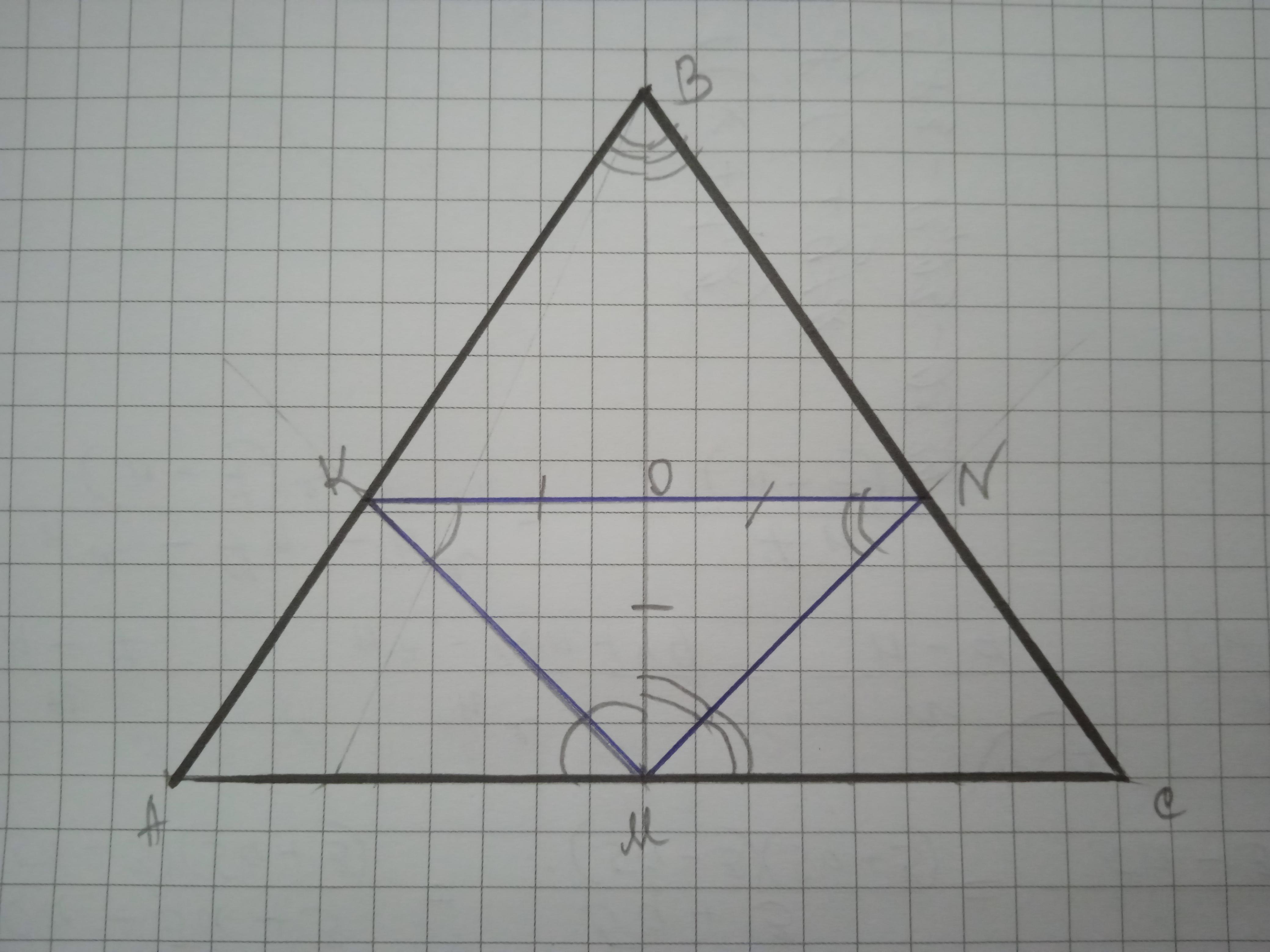
в треугольнике ABC провели биссектрису BM , а в треугольниках ABM и CBM - биссектрисы MK и MN соответственно, оказалось, что KN параллельно AC. найдите уголт MKN
​

Answer 1

Ответ:

45°

Объяснение:

∠АМК=∠МКN; ∠KNM=∠CMN;  ∠АВМ=∠СВМ по определению биссектрисы.

∠МКN=∠ВМК как внутренние накрест лежащие при KN║АС и секущей КМ;  ΔКОМ - равнобедренный; КО=ОМ

∠СМN=∠KNМ как внутренние накрест лежащие при KN║АС и секущей МN; ΔМОN - равнобедренный; ОN=ОМ

из этого следует, что ΔКОМ=ΔNОМ, значит, ∠МКN=∠NКМ, а ∠КМN=2∠МКN

Пусть ∠МКN=x°, тогда х+х+2х=180;  4х=180;  х=45.

∠МКN=45°

Answer 2

Ответ:

В файле. m77m

Объяснение: