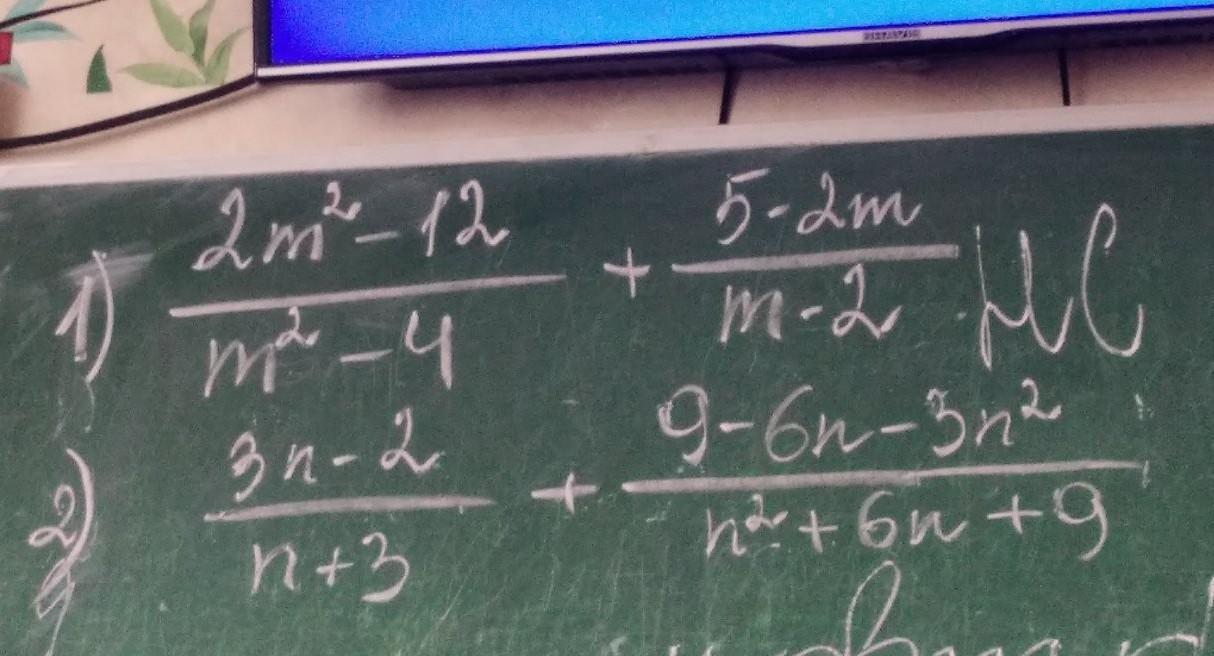Ответы
Ответ дал:
1
Ответ:
Объяснение:
1) =(2m^2 -12)/(m-2)(m+2) + (5-2m)/(m-2) =(2m^2-12+(m+2)*(5-2m)/(m-2)(m+2)=
(2m^2-12+5m-2m^2+10-4m)/(m-2)(m+2)=(m-2)/(m-2)(m+2) =1/(m+2)
( ^ -знак степени)
можно ещё второе пожалуйста?
Ответ дал:
1
огромное спасибо
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад