Question

9.4 В треугольнике ABC длина стороны AB равна 6, а длина стороны AC - 8. Медианы BN и CM этого треугольника взаимно перпендикулярны. Найдите сторону BC треугольника ABC. ПОМОГИТЕ СРОЧНО ПОЖАЛУЙСТА!!!

Answer 1

Ответ:

BC = 2√5

Объяснение:

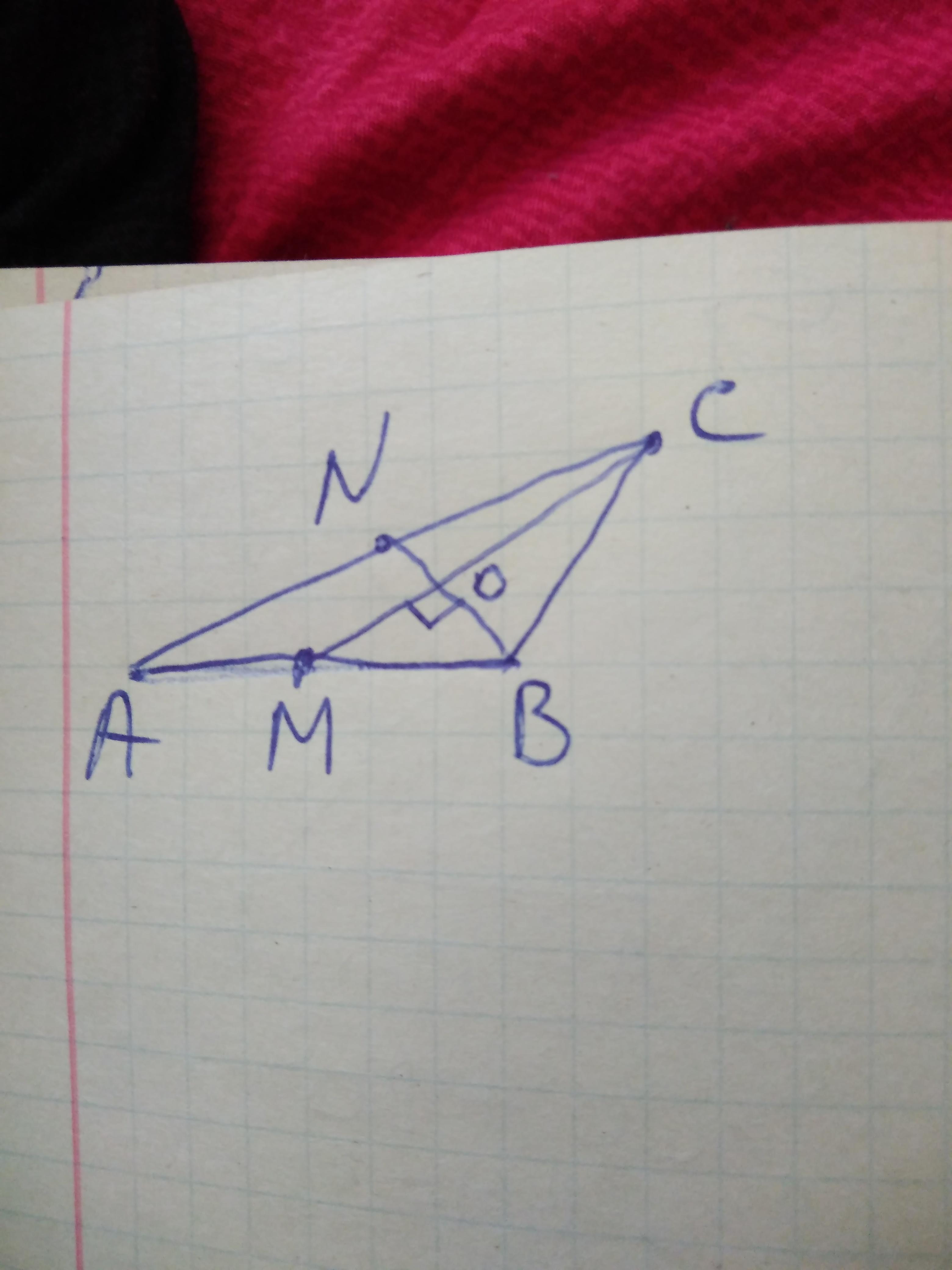
Чертеж на рисунке. Нам известно:

AB = 6; AM = MB = 3

AC = 8; AN = NC = 4

Найти: BC = x

Точку пересечения медиан обозначим О.

По свойству медиан:

BO = 2*ON; CO = 2*OM (1)

По теореме Пифагора:

BO^2 + OM^2 = BM^2 = 3^2 = 9

ON^2 + CO^2 = CN^2 = 4^2 = 16

BO^2 + CO^2 = BC^2

Подставляем равенства (1) в эти уравнения:

4*ON^2 + OM^2 = 9

ON^2 + 4*OM^2 = 16

Складываем уравнения:

5*ON^2 + 5*OM^2 = 25

Делим на 5:

ON^2 + OM^2 = 5

ON^2 = 5 - OM^2

Подставляем в любое уравнение:

5 - OM^2 + 4*OM^2 = 16

3*OM^2 = 11

OM^2 = 11/3

ON^2 = 5 - OM^2 = 5 - 11/3 = 4/3

Возвращаемся к равенствам (1):

BO^2 = (2*ON)^2 = 4*ON^2 = 4*4/3 = 16/3

CO^2 = (2*OM)^2 = 4*OM^2 = 4*11/3 = 44/3

BC^2 = BO^2 + CO^2 = 16/3 + 44/3 = 60/3 = 20

BC = √20 = 2√5