Ответы
Ответ дал:
1
Ответ:
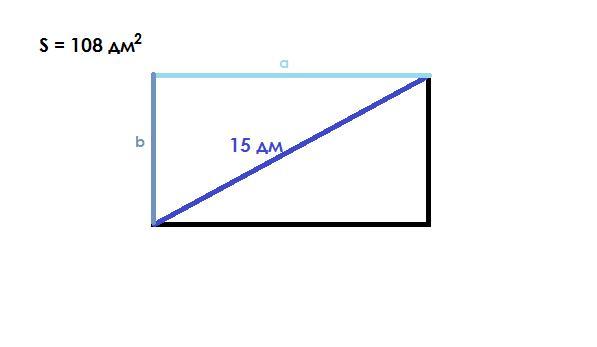
12 дм и 9 дм
Объяснение:
по т. Пифагора: a² + b² = 15²
по формуле площади: a * b = 108 ⇒ a = 108/b
подставим в первую формулу.
b² = t - новая переменная
b² = t - новая переменная
b² = 81 или b² = 144
b₁ = 9 b₂ = 12
найдем а.
a = 108/b
a₁ = 108/9 = 12
a₂ = 108/12 = 9
Стороны прямоугольника равны 12 дм и 9 дм
Приложения:
snyatkivskaya015:
Господи, спасибо огромное
Вас заинтересует
2 года назад
2 года назад
3 года назад
8 лет назад
10 лет назад
10 лет назад