Докажите:
Докажите:
Докажите:
Ребят, желательно по подробнее, я хочу понять
Пожалуйста (

Приложения:

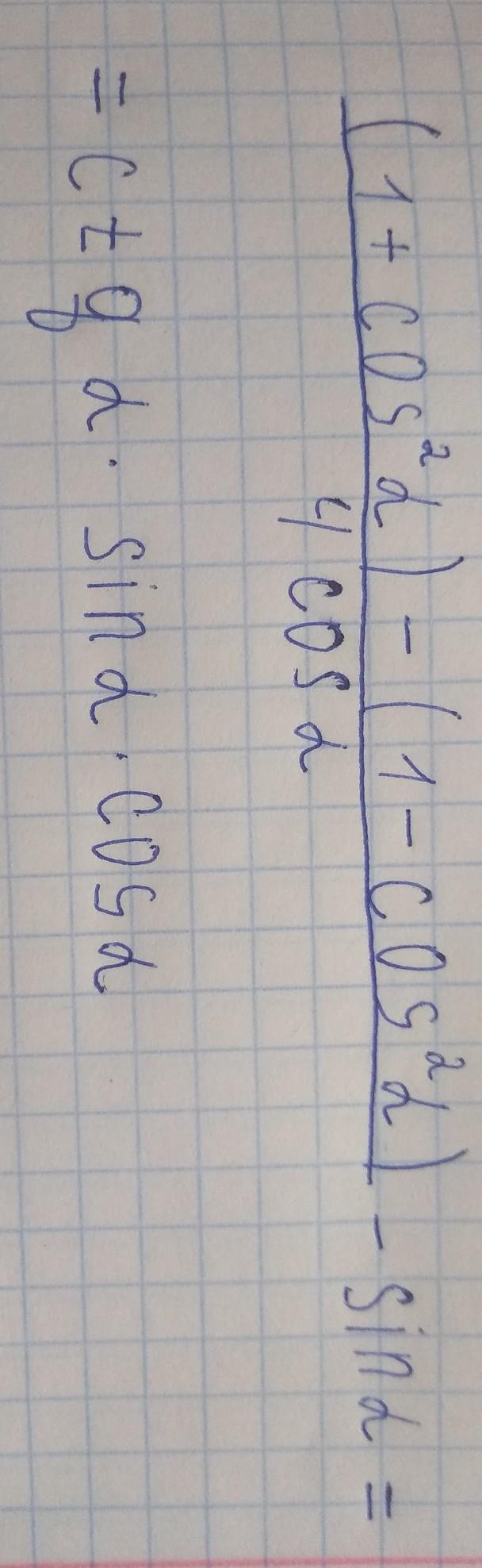
Аноним: да я незнаю как это делается я в 7 классе

Аноним: В 10 узнаешь

Аноним: хорошо спасибо что сказал

Аноним: ✔✔✔

Аноним: Нужно левую часть преобразовать, чтобы оно было похоже на правую. С тригонометрическими тождествами

Аноним: ты мне?

Аноним: ну я вообще тут ничего не понимаю извини

Аноним: я маленькая ещё ахахах ну реально не для меня

LFP: а у вас выражение ВЕРНО переписано...?? справа получается косинус в квадрате... а слева ничего похожего)) лучше фото задания...

Аноним: Все правильно, сам аху ел

Ответы

Ответ дал: NNNLLL54

Ответ:

$\star \ \displaystyle \frac{(1+cos^2a)-(1-cos^2a)}{4\, cosa}-sina=\frac{2cos^2a}{4\, cosa}-sina=\frac{cosa}{2}-sina=\\\\\\=\frac{cosa-2sina}{2}\ ;\\\\\\\star \ ctga\cdot sina\cdot cosa=\frac{cosa}{sina}\cdot sina\cdot cosa=cos^2a=\frac{1+cos2a}{2}\ ;\\\\\\\star \ \ \frac{cosa-2sina}{2}\ne \frac{1+cos2a}{2}$

$\displaystyle \star \ \ \frac{(1+cos^2a)-(1-cos^2a)}{4\, cosa}-sina=\frac{1+(cos^2a-sin^2a)}{4\, cosa}-sina=\\\\\\=\frac{1+cos2a}{4\, cosa}-sina=\frac{1+cos2a-4sina\, cosa}{4\, cosa}\ \ne \frac{1+cos2a}{2}$