Question

ПОМОГИТЕ РЕШИТЬ 3 ЗАДАНИЕ ПО ГЕОМЕТРИИ!!! ДАЮ 50 БАЛЛОВ!!

Answer 1

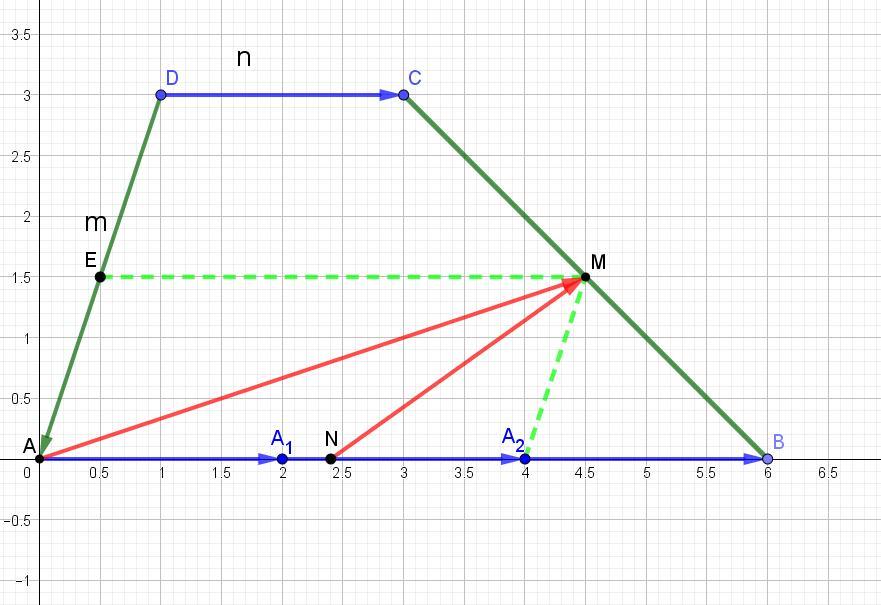
Точка М лежит на средней линии трапеции, которая делит и вектор m пополам.

Поэтому вектор AM = 2n - (1/2)m.

Находим положение точки N из условия AN : NB = 2 : 3.

То есть AN = (2/5)АВ, но АВ = 3n, поэтому AN = (2/5)*3n = (6/5)n.

Вектор NA2 = 2n - AN = 2n - (6*5)n = (10-6)/5n = (4/5)n.

Тогда вектор NM = NA2 + A2M = (4/5)n - (1/2)m.