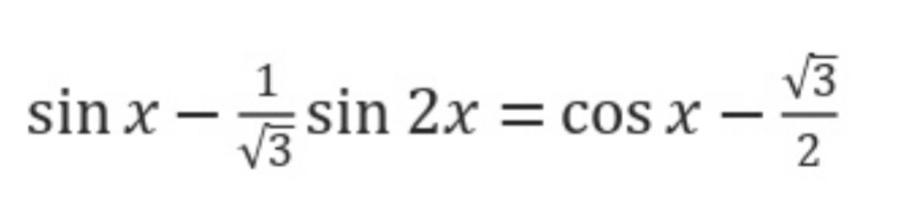Ответы
Ответ дал:
0
Ответ:
x1 = +-π/6 + 2πn, n ∈ Z; x2 = (-1)^k*(-π/3) + πk, k ∈ Z
Объяснение:
1)
x1 = +-π/6 + 2πn, n ∈ Z
2)
x2 = (-1)^k*(-π/3) + πk, k ∈ Z
Вас заинтересует
2 года назад
2 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад