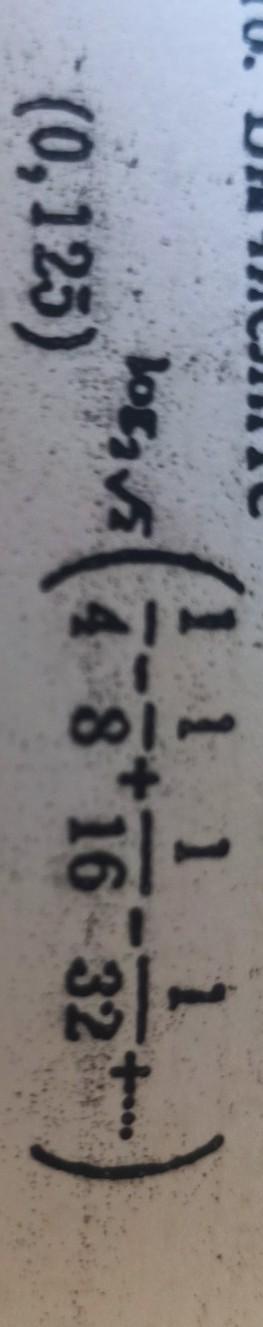Ответы
Ответ дал:
2
Ответ:
Пошаговое объяснение:
заметим, что является бесконечно
убывающей геометрической прогрессией
тогда
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
10 лет назад