Question

Найти стороны параллелограмма, если его периметр равен Р=36 см​

Answer 1

Ответ:

Объяснение:

Дано АВСД- пар-мм.

Р(АВСД)=36; ЕД=4

<ЕАД=30. ( см рис12)

Найти:. АВ=?;. АД=?

Решение;

∆АЕД ;. <Е=90; <А=30; ЕД=8;

=> АД = 2ЕД =8 ( катет против угла в 30 градусов)

Р= 2(АВ+АД)

АВ= Р/2 - АД

АВ = 36/2 - 8 = 10

Ответ. АВ=СД = 10

АД=ВС=8

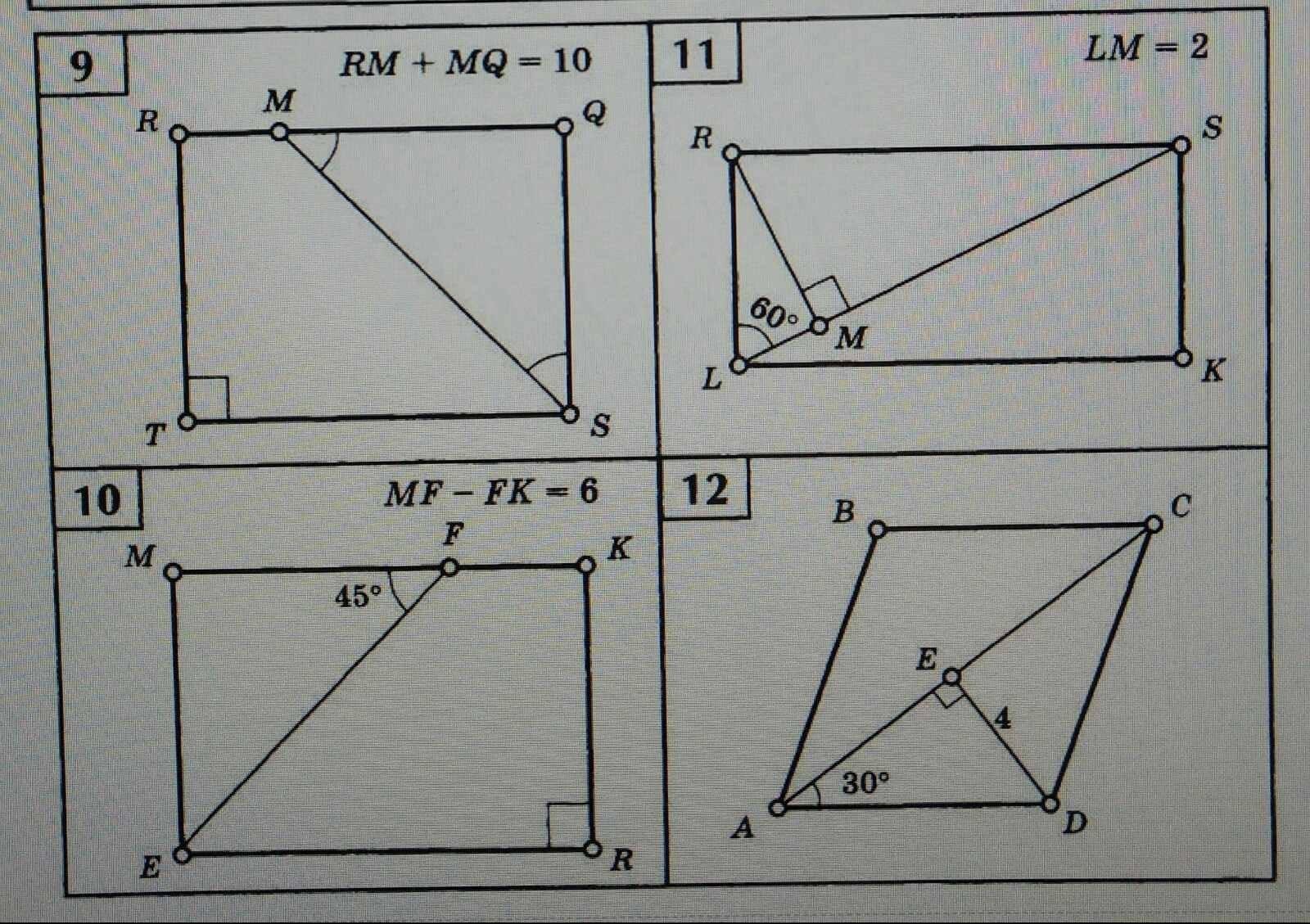
9) примем для простоты преобразований и меньшей писанины a=QS,. b=ST

P=36,. P=2(a+b);. b=a+x=10

MR = x

Составляем ур-е;.

2(10+10-х)=36

20-х=18

х=2

а = 10-2 =8,.

Ответ. а=QS=8;. b=ST=10

10) MF - FK = 6

ME=MF (два катета равнобедренного ∆).

Примем меньшую сторону за х

МF= х

FK= x+6

Составляем уравнение

2(х+х+6)=36;. х=( 18-6)/2=6.

Ответ: МF=6;. FK=6+6=12