Установить сходимость или расходимость следующих последовательностей, а в случае сходимости вычислить предел:
Приложения:
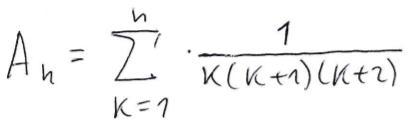
Ответы
Ответ дал:
17
Ответ:
;
Пошаговое объяснение:
Разложим член ряда на простейшие дроби:
Значит,
Преобразуем:
,
.
Подставляем:
При этом - а это означает, что
den2591:
помоги с алгеброю, у меня кр, что бы сдать осталось 10 мин
Ответ дал:
15
Чтобы не использовать в э той задаче метод неопределенных коэффициентов, воспользуемся формулой, которая проверяется непосредственно, легко запоминается и много раз помогала мне в вычислениях:
В частности,
Имеем:
Можно было рассуждать немного иначе: k+1=t;
при
Ответ: последовательность сходится, и ее предел равен
какой это класс я только в пятом Инфина задание
нифига
ВЫДАЮЩИЙ ЛИЧНОСТЬ ПО ОБЩЕСТВОЗНАНИЮ 6 КЛАСС
цук
Вас заинтересует
2 года назад
3 года назад
3 года назад
10 лет назад
10 лет назад