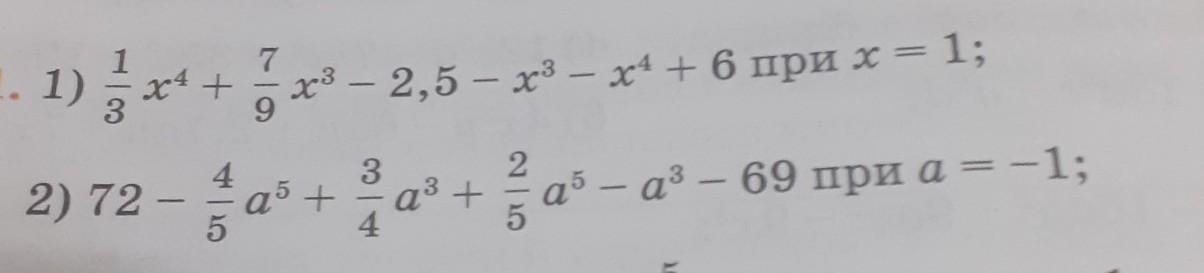Ответы
Ответ дал:
1
Ответ:
надеюсь верно
или( хз можно ли так сокращать)
KryZnani:
Спасибо
писал через редактор формул, так что не исключены ошибки
ок
добавил альтернативу
Ок добавлю
Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
10 лет назад