Ответы
Ответ дал:
0
Ответ: 9 (ед. длины)
Объяснение:
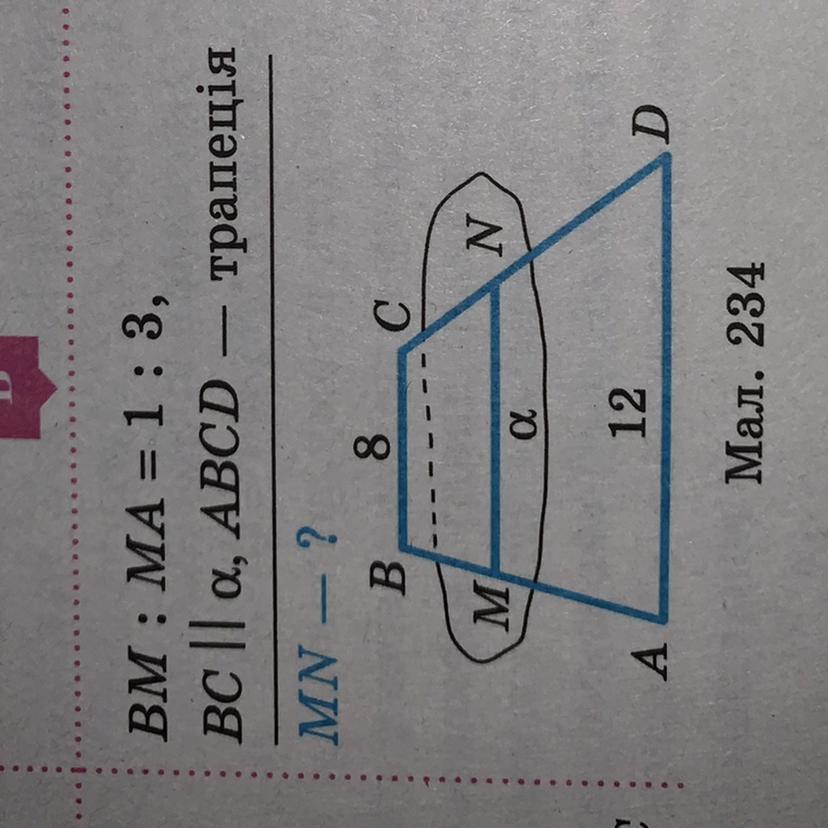
Из условия MN||BC => MN||AD.
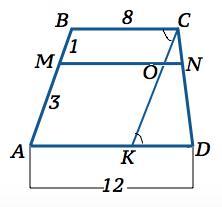
Из вершины трапеции С проведем прямую параллельную АВ до пересечения с АD в т. К . Пусть О -точка пересечения СК и MN.
АВСD - трапеция, => основания ВС||AD.
Поскольку MN=α, ВС||α ( дано), то ВС||MN; СО||ВМ (по построению),=> четырехугольники MBCО и АВСК – параллелограммы и МО=АК=ВС=8.
По т. Фалеса о пропорциональных отрезках параллельные прямые отсекают на секущих пропорциональные отрезки. => CN:ND=BM:MA=1:3
ВС||AD => В ∆ КСD отрезок ON||KD =>.
∆ CON~∆ CKD; k=CN:CD=1:(CN+ND)=1:4
ON=KD•k=4•1/4=1
MN=MO+ON=8+1=9 (ед. длины).
Приложения:
Вас заинтересует
3 года назад
8 лет назад
8 лет назад
9 лет назад