СРОЧНО!!!!
в треугольнике ABC AA1 и CC1- биссектрисы. Оказалось, что угол АА1С = 2угла АС1С. Чему равен угол ВАС
Ответы
Ответ дал:
0
Ответ:
120°
Объяснение:
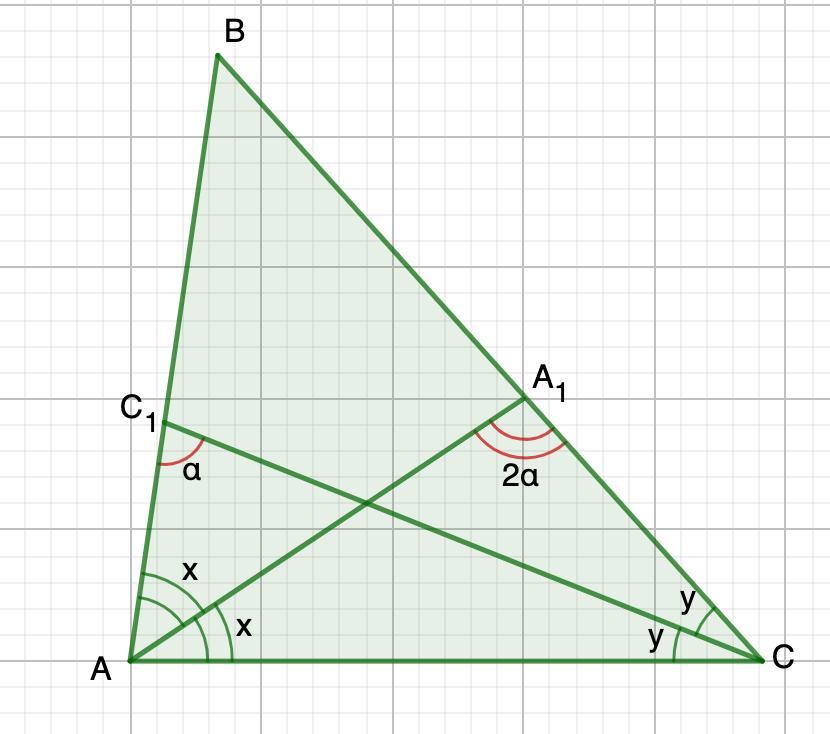
Дано: ΔАВС.
АА₁ и СС₁ - биссектрисы.
∠АА₁С=2∠АС₁С
Найти: ∠ВАС
Решение:
Пусть ∠ВАА₁=∠А₁АС=х и ∠ВСС₁=∠С₁СА=у (АА₁ и СС₁ - биссектрисы)
Если ∠АС₁С=α, то ∠АА₁С=2α (условие)
- Сумма уголов треугольника равна 180°.
Рассмотрим ΔАС₁С.
α+2х+у=180°
или
α=180°-2х-у
Умножим обе части равенства на 2:
2α=360°-4х-2у
Рассмотрим ΔАА₁С.
2α+х+2у=180°
или
2α=180°-х-2у
Получили два равенства:
2α=360°-4х-2у и 2α=180°-х-2у
- Если левые части равенств равны, то и правые равны:
360°-4х-2у=180°-х-2у
3х=180°
х=60°
∠ВАС=2х=120°
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
9 лет назад