Question

ПОМОГИТЕ! 43 БАЛЛА ДАМ! ПОДРОБНЫЕ
ПОМОГИТЕ! 43 БАЛЛА ДАМ! ПОДРОБНЫЕ (ЖЕЛАТЕЛЬНО) ОТВЕТЫ!
1 задание
Высота
остроугольного треугольника АВС образует со сторонами, выходящими из
той же вершины, углы 18 градусов и 46 градусов. Найдите углы
треугольника АВС
2 задание
Докажите равенство прямоугольных треугольников по гипотенузе и острому углу
3 задание
(Там текст не видно, напишу здесь)
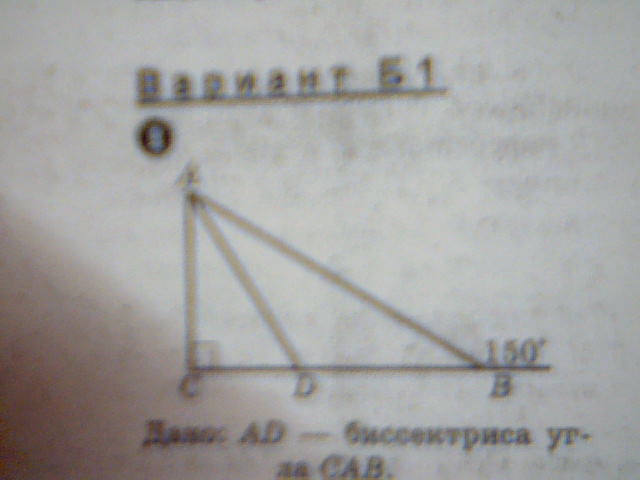
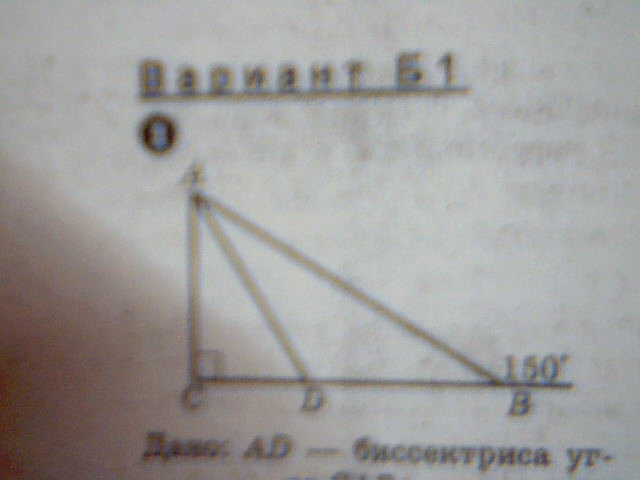
Дано: AD-биссектриса угла САВ
Найти: острые углы треугольника ACD
Чертеж на картинке

Answer 1

1) 90-18=72 и 90-46=44
2)Если гипотенуза и острый угол одного треугольника   соответственно   равны гипотенузе и острому углу другого треугольника, то такие прямоугольные треугольники равны.  Чтобы доказать эту теорему, построим два прямоугольных гольника ABC и А'В'С', у которых углы А и А' равны, гипотенузы АВ и А'В' также равны, а углы С и С' — прямые    Наложим треугольник А'В'С' на треугольник ABC так, чтобы вершина А' совпала с вершиной А, гипотенуза А'В' — с равной гипотенузой АВ. Тогда вследствие равенства углов A и А' катет А'С' пойдёт по катету АС; катет В'С' совместится с катетом ВС: оба они перпендикуляры, проведённые к одной прямой АС из одной точки В (§ 26,следствие 3). Значит, вершины С и С' совместятся. Треугольник ABC совместился с треугольником А'В'С'. 
Следовательно, / АВС = / А'В'С'. Эта теорема даёт 3-й признак равенства прямоугольных треугольников (по гипотенузе и острому углу).
3)угол САД=30 а угол СДА=60