Question

Крест, состоящий из двух одинаковых больших и двух одинаковых маленьких квадратов, поместили внутрь ещё большего квадрата. Вычислите в сантиметрах сторону самого большого квадрата, если площадь креста — 490 см 2.

Дам 40 балов

Answer 1

Ответ:

28 см

Пошаговое объяснение:

S = (S1 + S2) * 2 - общая площадь

S1 = a1 * a1 = a1² - площадь 1 маленького

S2 = a2 * a2 = a2² - площадь 1 среднего

Подставляем:

S = (a1² + a2²) * 2

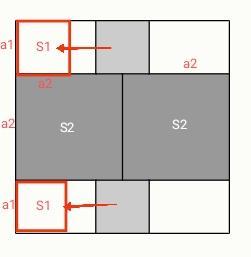
Если сместить 2 маленьких квадрата влево (как на моей картинке), получим, что сторона большего квадрата равна сумме 2 сторон маленьких квадратов (a1 + a1) и 1 стороны среднего квадрата (a2).

Если мы сместим 2 средних квадрата вниз, то получим, что сторона большого квадрата равна 2 сторонам средних квадратов (a2 + a2).

Приравниваем значения:

a1 + a1 + a2 = a2 + a2

a2 = 2 * a1

Подставим:

S=(a1² + 4 * a1²) * 2 = 490

5 * a1² = 245

a1² = 49

a1 = √49 = 7

a2 = 2 * a1 = 14

l = a1 + a1 + a2 = 28 см

Точно такое же решение идёт с площадью 810 см²