Ответы
Ответ дал:
0
Ответ:
Аноним:
Помоги ищё зайди в мои вопросы
спасибо за этот пример ещё не нажал
Ответ дал:
1
::::::::::Объяснение::::::::::
Приложения:
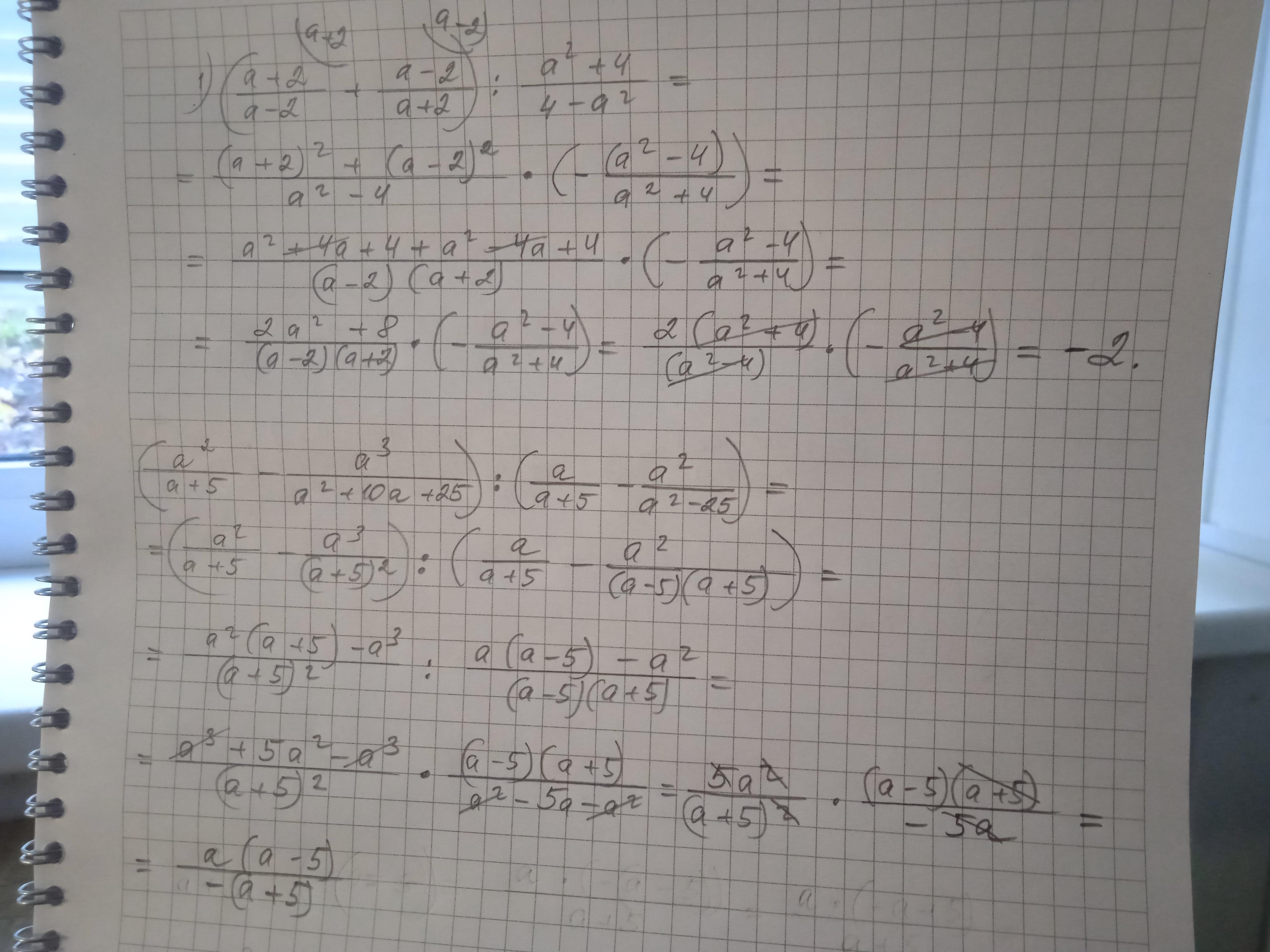
Поможешь ищё зайди в мои вопросы там тоже 100 балов даю
Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
9 лет назад