Question

Четырехугольник ABCD - трапеция, уголA = 64°. Найдите угол между векторами BA и AD​

Answer 1

Объяснение:

Дано: ABCD - трапеция;

∠А=64°

$\overrightarrow{BA};\;\overrightarrow{AD}.$

Найти: угол между векторами BA и AD​.

Решение:

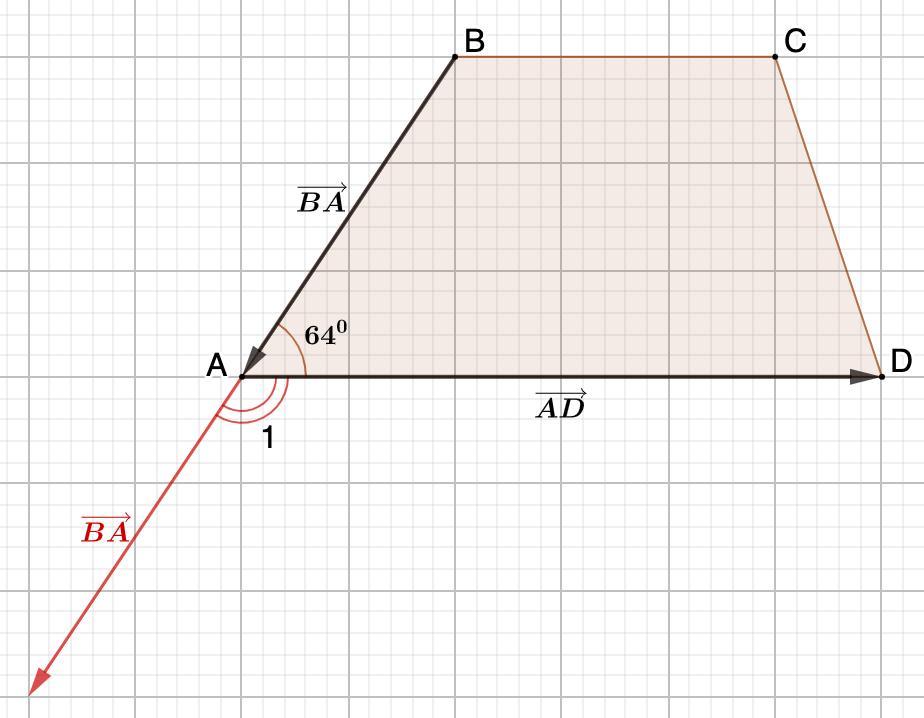
• Чтобы найти угол между векторами, надо отложить их из одной точки путем параллельного переноса.

Продлим сторону ВА на длину вектора ВА.

Искомый угол - ∠1.

• Сумма смежных углов равна 180°.

⇒ ∠А+∠1=180° (смежнае)

Отсюда ∠1=180°-∠А=180°-64°=116°