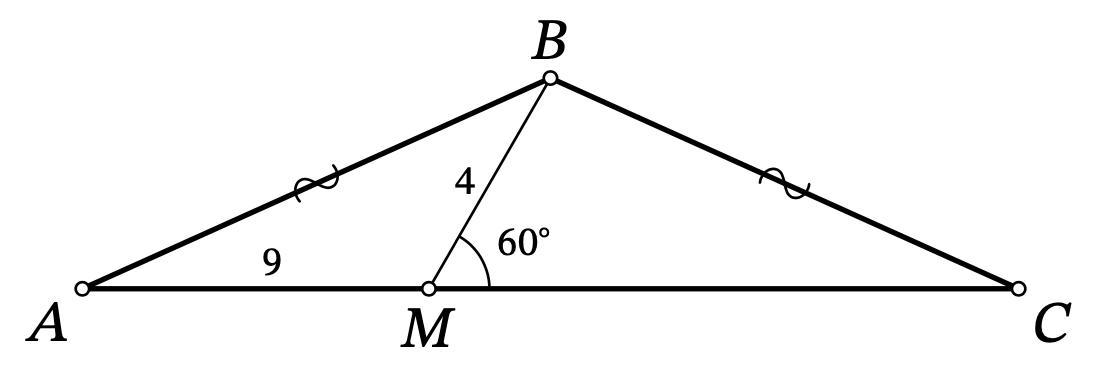
На основании AC равнобедренного треугольника ABC (AB=BC) отмечена точка M. Известно, что AM=9, MB=4, ∠BMC=60∘. Найдите длину отрезка AC.
Приложения:
habibolaev0:
где ответ ээээээ
дай да ответ
дай дапаааааааа
Ответы
Ответ дал:
1
Ответ:
22 ед.
Объяснение:
Дано: ΔABC (AB=BC) - равнобедренный.
AM=9, MB=4, ∠BMC=60°.
Найти: АС
Решение:
Проведем высоту ВН.
Рассмотрим ΔМВН - прямоугольный.
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒∠МВН=90°-∠ВМН=90°-60°=30°
- Катет, лежащий против угла в 30°, равен половине гипотенузы.
⇒МН=ВМ:2=4:2=2
АН=АМ+МН=9+2=11
- В равнобедренном треугольнике высота является медианой.
⇒АН=НС=11
Тогда
АС=АН+НС=11+11=22 (ед)
Приложения:

Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
10 лет назад
10 лет назад