Question

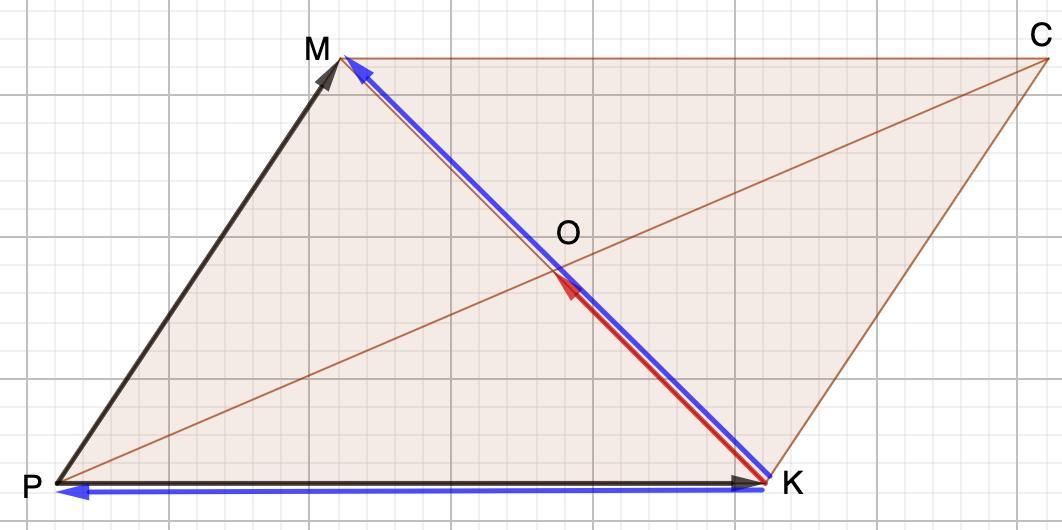
Диагонали параллелограмма РМСК пересекаются в точке О. Выразите вектор КО через векторы РК и РМ​

Answer 1

Объяснение:

Дано: РМСК - параллелограмм;

РС ∩ МК=0

$\displaystyle \overrightarrow{KO};\; \overrightarrow{PK} ;\;\overrightarrow{PM}$

Выразить вектор КО через векторы РК и РМ​.

Решение:

По правилу треугольника:

$\overrightarrow{KP}+\overrightarrow{PM}=\overrightarrow{KM}$

Так как

$\overrightarrow{KP}=-\overrightarrow{PK}$

Получим

$\overrightarrow{PM}-\overrightarrow{PK}=\overrightarrow{KM}$

• В параллелограмме диагонали точкой пересечения делятся пополам.

⇒

$\displaystyle \overrightarrow{KO}=\frac{1}{2}\overrightarrow{KM}$

или

$\displaystyle \overrightarrow{KO}=\frac{1}{2}(\overrightarrow{PM}-\overrightarrow{PK})$